0320

321

§ 2. Funkcje ciągle

Wówczas jednak na mocy (5) będzie także \f(x₁,x₂, ...,x_n)-f(x'_l,x'₂, ...,x')| =

=    ,t₂,... ,f_m), ..., ę_n{ti,t₂, .... ,t_mj)-f(ę_l{t\ ,t'₂,... ,t'_m),, <p_n(t\ ,ł₂.....0)|<£

co stanowi dowód naszego twierdzenia.

171. Funkcje ciągle w obszarze. Twierdzenia Bolzano-Cauchy’ego. Będziemy mówili, że funkcja/(x,, ..., x„) jest ciągła w pewnym zbiorze J( punktów przestrzeni n-wymia-rowej, jeśli jest ona ciągła w każdym punkcie tego zbioru, który jest jego punktem skupienia. Będziemy się odtąd ograniczali do przypadku, gdy zbiór J( jest obszarem otwartym lub domkniętym [163], podobnie jak funkcje ciągłe jednej zmiennej rozpatrywaliśmy w przedziale.

Zajmiemy się teraz badaniem własności funkcji wielu zmiennych, ciągłej w pewnym obszarze przestrzeni «-wymiarowej. Własności te są zupełnie analogiczne do własności funkcji jednej zmiennej ciągłej w przedziale (rozdział II, §5).

W wykładzie ograniczymy się dla krótkości jedynie do przypadku dwóch zmiennych niezależnych. Przenosi się to wszystko bez trudu bezpośrednio na przypadek ogólny.

Zresztą pewne uwagi na ten temat zrobimy przy sposobności.

Sformułujemy obecnie twierdzenie analogiczne do pierwszego twierdzenia Bolzano--Cauchy’ego dla funkcji jednej zmiennej [80].

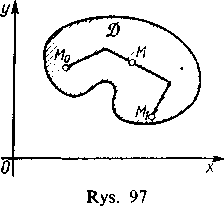
Twierdzenie. Niech funkcja f (x, y) będzie określona i ciągła w pewnym obszarze spójnym 2. Jeśli w dwóch punktach M₀(x₀. y₀) i M,(x₁, yj) tego obszaru funkcja przybiera wartości o różnych znakach

f(^xo > >’₀)<0 ,    /(x,, y,)>0 ,

to w obszarze tym istnieje również punkt M'(x', yj, iv którym funkcja ta jest równa zeru,

/(*', /)=o.

Dowód przeprowadzimy przez sprowadzenie do przypadku funkcji jednej zmiennej niezależnej.

Wobec spójności obszaru 2 punkty M₀ i M₁ można połączyć krzywą ciągłą, mianowicie łamaną, której wszystkie punkty leżą w 2 (rys. 97).

Jeśli będziemy kolejno badali wierzchołki tej łamanej, to albo okaże się, że w którymś z nich funkcja jest równa zeru i wówczas twierdzenie jest udowodnione, albo tak nie będzie. W tym ostatnim przypadku znajdzie się bok łamanej, na którego końcach funkcja przybiera wartości różnych znaków. Zmieniając oznaczenia punktów, przyjmiemy, że M₀ i Afj są właśnie końcami tego boku. Jego równanie ma postać [161]:

x = x₀ + t(xj — x₀), y = yo + *0’i-J'o)    (0<f<l).

Gdy punkt M(x, y) porusza się wzdłuż tego boku, nasza wyjściowa funkcja / (x, y) staje

21 G. M. Fichtenholz