0502

503

§ 4. Długość krzywej płaskiej

lub krócej: (10)

s',=slx’_t²+y’_t².

Jeżeli podniesiemy tę równość obustronnie do kwadratu i pomnożymy przez dt², to otrzymamy wzór o bardzo prostej postaci

(11)    ds² — dx² + dy²,

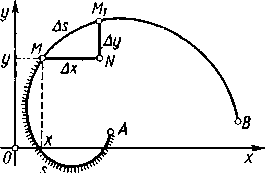
który ponadto ma poglądowy sens geometryczny. Na rysunku 152 w krzywoliniowym trójkącie prostokątnym MN Mi „przyprostokątnymi” są MN=dx, NM_t=Ay — przyrosty współrzędnych punktu M, a „przeciwprostokątną” łuk MM i—As, który jest przyrostem łuku AM—s. Okazuje się, że wprawdzie nie dla samych przyrostów, lecz dla ich części głównych — różniczek spełnione jest swego rodzaju twierdzenie Pitagorasa.

Należy wyróżnić specjalne przypadki wzoru (10) odpowiadające różnym sposobom przedstawienia krzywej. Tak więc, gdy krzywa przedstawiona jest równaniem y=f{x) we współrzędnych kartezjaóskich, to rolę parametru gra x i łuk s jest funkcją zmiennej x. Wzór (10) przybiera postać

(lOa)    sWi+7¹:

Przedstawienie krzywej równaniem r=g(9) we współrzędnych biegunowych jest, jak wiemy, równoważne z przedstawieniem parametrycznym

x = rcos0_i, y = rsin0,

w którym parametrem jest kąt 0. Łuk jest teraz funkcją s=s(9) zmiennej 9. Ponieważ x'_t=r_g cos 0 — r sin 0, yi=rś sin 0+r cos 0,

więc

x'g²+y'_e² = r'„² + r*

i wzór (11) przybiera postać (lOb)    sJ = V r'₉² + r².    Rys. 152

Często wygodnie jest obrać jako punkt początkowy A dla liczenia długości łuku nie jeden z końców rozpatrywanego łuku krzywej, lecz jakikolwiek jego punkt wewnętrzny. W tym wypadku naturalne jest przyjmować łuki odkładane od niego w stronę wzrastania parametru za dodatnie, a odkładane w przeciwną stronę — za ujemne i odpowiednio do tego, długości łuku w pierwszym przypadku nadawać znak plus, a w drugim minus. Tę właśnie długość łuku s ze znakiem będziemy dla krótkości nazywali po prostu lukiem. Wzory (10), (11), (lOa) i (lOb) są prawdziwe dla wszystkich przypadków.

Zauważmy, że jeśli dodatni zwrot dla obliczania łuków weźmie się nie w stronę wzrastania parametru, jak się to zwykle robi, lecz w stronę, w którą parametr maleje, to we wzorach (10), (lOa) i (lOb) trzeba przed piefwiastkiem postawić znak minus.