0504

505

§ 4. Długość krzywej płaskiej

Przyjmijmy łuk jako parametr i niech punkt M odpowiada wartości s łuku, a punkt M, wartości s+As. Współrzędnymi tych punktów niech będą (x, y) i (x+Ax, y+Ay). Wówczas

^ MM, = \As\,    MM ,=\1ax²+Ay² ,

a więc

MM, -sjAb^+Ay² l(~Ax\² /Ay\²

~ mm, pTj v 1.77) ⁺\ J7y'

Przechodząc do granicy przy As-*0 otrzymujemy dowodzoną równość na podstawie wzoru (12).

Dotychczas położenie stycznej do krzywej w punkcie zwykłym M określaliśmy współczynnikiem kierunkowym tg a, nie rozróżniając dwóch przeciwnych zwrotów, jakie mogą być obrane na stycznej — współczynnik tg a był dla obu ten sam. W pewnych badaniach jednak okazuje się konieczne wyróżnienie jednego z tych zwrotów.

Przypuśćmy, że na krzywej wybrany jest punkt początkowy i określony jest zwrot dla liczenia łuku. Przyjmijmy łuk jako parametr określający położenie punktu na krzywej.

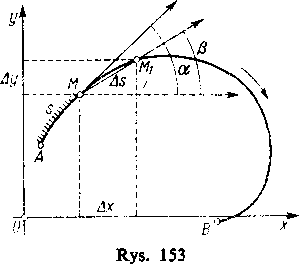
Niech punktowi M, o którym mówimy, odpowiada łuk s. Jeżeli nadamy łukowi s dodatni przyrost As, to łuk s+As określi nowy punkt M, leżący od M w stronę wzrastania łuku. Nadajmy siecznej MM, zwrot od M do M, i oznaczmy przez /? kąt, który sieczna o tym zwrocie tworzy z dodatnim kierunkiem osi x. Rzutując odcinek MM, na osie układu (rys. 153) otrzymujemy na podstawie znanego twierdzenia z teorii rzutów

rzut* MM ,—Ax=MM, cos /?,

rzut,, MM i=Ay—MM, sin p,

skąd

cosj?=-

Ax

sin/f-

Ay

MM,    MM,

Ponieważ '-'MM,—As, więc równości te można przepisać w postaci

„ Ax - MM, cos 8——- —

^r /fc

(14)

sin fi-

As MMj Ay ^ MM,

As MM,

Będziemy nazywali dodatnim ten zwrot stycznej, który wskazuje w stronę wzrastania łuku. Ściślej mówiąc, styczną ze zwrotem dodatnim otrzymujemy jako położenie graniczne,