090

6. Testowanie hipotez

której rozkład, dokładny lub przybliżony, jest znany przy założeniu prawdziwości hipotezy H₀. Następnie wyznaczamy obszar Q C R służący do weryfikacji hipotezy H₀ w ten sposób, aby przy założeniu prawdziwości H₀ była spełniona równość

Pr (ZeQ) - a.    (6.1.1)

Wtedy odrzucamy H₀ i przyjmujemy H_{, o ile istotnie zdarzy się, że z — Z (co) = z(x i,jc₂, ... E Q, czyli, gdy zajdzie zdarzenie mało prawdopodobne. W praktyce statystycznej przyjmuje się zwykle, że a — 0.05, czasem a = 0.01 lub ewentualnie a = 0.1.

Obszar krytyczny i poziom istotności

Obszar Q nazywa się obszarem krytycznym, a liczbę a nazywa się poziomem istotności. Hipotezę zerową odrzucamy na korzyść alternatywnej, gdy wartość z statystyki Z znajdzie się w obszarze krytycznym. Może się oczywiście zdarzyć, że z € Q mimo, że hipoteza H₀ jest prawdziwa. Zdarzy się to jednak z małym prawdopodobieństwem a. Popełniamy wtedy błąd polegający na odrzuceniu hipotezy prawdziwej, zwany błędem pierwszego rodzaju. Przyjęcie hipotezy H₀ fałszywej stanowi błąd drugiego rodzaju. W przyjętej tutaj procedurze nie ma jednak przyjmowania H₀, co najwyżej postanawia się, że nie ma podstaw do jej przyjęcia. Taką procedurę postępowania przyjęto, gdyż nie precyzuje się tu prawdopodobieństwa popełnienia błędu drugiego rodzaju. W następnych punktach omówimy przykłady testów statystycznych, gdzie nieznanymi parametrami próby będą wartość oczekiwana i wariancja. Liczne przykłady innych testów można znaleźć w książce [5].

6.1.1. Testy dla średniej

Podobnie jak dla przedziałów ufności, rozpatrujemy trzy modele: rozkład normalny ze znaną wariancją, rozkład normalny z nieznaną wariancją, rozkład dowolny ze skończoną wariancją i duża próba. We wszystkich modelach n oznacza liczebność próby.

Rozkład normalny, <T znane

Model I. Populacja generalna ma rozkład N(m,a), odchylenie standardowe jest znane. Nieznany jest parametr m, dla którego stawiamy hipotezę H₀ : m — m₀, przeciwko jednej z hipotez:

H| : m 7^ nią,

H_[ : m > m₀,

H | : m < m₀.

Statystyka służąca do weryfikacji hipotezy H_Q dana jest wzorem

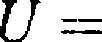
X — m

o

a

i

(6.1.2)