126 127 (3)

Przestrzenie euklidesowe

gwarantującego równość przestrzeni

lin {iii, u₂, i*3} = lin {£1, £2, £3},

oraz z warunków ortogonalności £3 _L v_{, £3 _L £2 Otrzymamy w tedy układ równań

f I £3, t’i) = 5 + 6 + 6c - 8 + 4A — 6c = 56 — 3 = 0 \ (®3, v₇) = 30 + 6fr + 36c-*-12-S6 + 9c-r4-f c = 46c + 46 = 0 '

Skąd mamy b = i, c = — 1. zatem £3 =    —J,3) .

b) Stosując ogólne wzory na ortogonahzację Grama-Schmićta otrzymujemy kolejno

v-2 = n₂

(*3, £?) _

l^l²

£,=*, = (1,0, 1,0)

(*2, V;)

|t5i|

(U₃,Sl),

^{V5 = U1}"W^V1

(—1,2,1,0),

n 1 ^v* ~ (3-3’

Znalezione wektory v\, v₂, £3 stanowią już bazę ortogonalną przestrzeni lin { u_:, u_2t £3} . Zauważmy, że rachunki w tym przykładzie można było jeszcze skrócić wykorzystując or-togonaJność wektorów ui i £3. Po przyjęciu dogodniejszej kolejności wektorowi zastosowaniu metody Grama-Schmidta otrzymalibyśmy £_: = £i, £2 = £3, £3 = (—1.1,1,—1). c) Stosując: ortogonalizację Grama-Schmidta do wektorów p_x, p₂, p₃ otrzymujemy wektory

<7. = 1,

2

r —

(*.*)

Ul²

(fli)

Ml²

1 = I

1 -

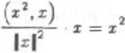
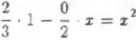
Wielomiany l,x,x — - tworzą zatem bazę ortogonalną przestrzeni lin danym iloczynem skalarnym.

2

‘ 3'

{l,J,x²} z po-

• Przykład 13.4

Podane wektory uzupełnić do baz ortogonalnych odpowiednich przestrzeni eukli-desowych:

a)    (1,4, -2), (2, —1, —1) w przestrzeni E³;

b)    (1,1,1,0). (0,1. —1,1) w przestrzeni E⁴;

c)    2z+l w przestrzeni Z?2[x] z iloczynem skalarnym wielomianów p = ax²-fóx-|-c, 9 = a\z² -f &ix + Ci, określonym wzorem (p, q) = aai + fchi + ccj.

Rozwiązanie

Oczywiście dane wektory muszą być ortogonalne. Najpierw uzupełnimy' je do zwykłej bazy rozważanej przestrzeni liniowej, a następnie bazę ort ogon ali żujemy zostawiając dane na początku wektory bez zmian.

a) Wektory v\ — (1,4,—2), £2 = (2,-1,-1) uzupełniamy do bazy przestrzeni E³ np o wektor £3 = (0.0,1). Stosując metodę Grama-Schmidta znajdujemy brakujący wektor

t»3 = U3 -

(£3, £1) -

|S.I^J

Trzynasty tydzień - przykłady

Zauważmy, że w tym przykładzie wektor £3 można wyznaczyć także ze wzoru ij = ti x S? ₌    —3, -9) łub też przyjąć £3 = (o, 6,c) i rozwiązać układ równań a + 4ł>- 2c = 0,

2a — b — c = 0.

b) Spośród wektorów bazy standardowej przestrzeni E^K dobieramy dwa wektory stanowiące wraz z danymi £1 = (1,1,1,0), £2 = (0,1,-1,1) bazę tej przestrzeni. Wektory ej = (0,0,1,0), ?4 = (0,0,0,1) są tu dobre, bowiem

1 1

0 1 0 0 0 0

1 0 1 1 1 0

0 1

= 1*0.

Dalsze wektory £3, £4 bazy ortogonalnej obliczamy ze wzoru

{h £1) _z (h, £2) -l*i|

V₂

l*2|²

ua = ej

= (0,0,1,0) — j(l, 1,1,0) + j(0,1,-1,1) = (-J.0. J.l) ,

a _ 2    (*«■»') =    _ (fiiiłis

⁴    '    |5.|² ‘    1*4    1*4

= CO.0.0.1) _ 0 - i (0,1. -1.1) - 1 (-i o, i. I) = (i,-1,0.1)

c) Wektor q_: = 2x41 uzupełniamy do bazy przestrzeni i?2(x] o wektory p- = l, P₃ = z² ■ Stosując wzory Grama-Schmidta obliczamy brakujące wektory q_2l ę₃ bazy ortogonalnej:

^{,ł =} 1'p^^{(2l + 1) =} 1"i^{(2l+,) =} '^ ⁺ ?’

<73 = r²,

bowiem (p₃, <7,) = (p₃. q₂) = 0.

• Przykład 13.5

Znaleźć bazy ortonormalne podanych przestrzeni euklićesowych i podać współrzędne wskazanych wektorów w tych bazach:

a)    E — {(x, y, z,t) G E⁴ : 4r — z = 2y — 3x — 2ż = 0}, v = (1, —3,4,9):

b)    E = Rt[x) z iloczynem skalarnym zdefiniowanym wzorem

Rozwiązanie

Najpierw wyznaczymy zwykłe bazy rozważanych przestrzeni liniowych, a następnie zor-togonalizujemy je i unormujemy. Współrzędne wektorów będziemy obliczać jak w Przykładzie 13.1. a) Zauważmy, że

E = ((z.y. 4z,6x - y) : z,y € i?} = lin ((1,0,4,6), (0,1,0, -1)} .