126 127 (3)

Przestrzenie euklidesowe

gwarantującego równość przestrzeni

lin {iii, U2, *3} = lin { Si, rh, S₃),

oraz z warunków ortogonalnośri t;₃ 1    , tij 1 Otrzymamy wtedy układ równań

f    = 5 + 6 + 6c - 8 + ib - 6c= 56 - 3 = 0

\(S_it S₂) = 30 + 6& + 36c^l2-S6 + 9c-r4 + c = 46c-f 46 = 0 '

Skąd mamy b = i, c = - J. zatem t'₃ = (—|, — i, 3) .

O

b) Stosując ogólne wzory na ortogonalizację Grama-Schmidta otrzymujemy kolejno

5] = *1 = (1,0,1,0)

V-₂ = U2 —

V3 = U3 ~

(»».”:) _a _

l^il^{2 5}

(“3, 61) „

l*i|^{2    1}

(-1,2,1.0).

(»3,gz)

r₂|²

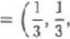
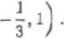
Znalezione wektory vi, V2, v₃ stanowią już bazę ortogonalną przestrzeni lin {u_:, 1*2, S₃} . Zauważmy, że rachunki w tym przykładzie można było jeszcze skrócić wykorzystując or-tagonalność wektorów ii i Po przyjęciu dogodniejszej kolejności wektorowi zastosowaniu metody Cl rama-Schmidt a otrzymalibyśmy    = Uj, t?₂ = €3, S3 = (—1.1,1,— 1).

c) Stosując ortogonalizację Grama-Schmidta do wektorów p₁₍ p₂, p₃ otrzymujemy wektory

<7; = 1.

- r

— “ i=x.

|1|²    3

(r³.l)    ,    («*.,)

m

1*1

Wielomiany 1 ,x,z — - tworzą zatem bazę ortogonalną przestrzeni lin danym iloczynem skalarnym.

2

“ 3'

{l . X, x² } 2 po-

• Przykład 13.4

Podane wektory uzupełnić do baz ortogonalnych odpowiednich przestrzeni eukli-desowych:

a)    (1,4, —2), (2, —1, —1) w przestrzeni E³;

b)    (1,1,1,0). (0,1, —1,1) w przestrzeni E^A.

c)    2r+l w przestrzeni jRj[x] z iloczynem skalarnym wielomianów p = az²+6x-ł-c, q = aiz² + biz + ci, określonym wzorem (p, q) = aai + bb\ + ccj.

Rozwiązanie

Oczywiście dane wektory muszą być ortogonalne. Najpierw uzupełnimy je do zwykłej bazy rozważanej przestrzeni liniowej, a następnie bazę ortogonalizujemy zostawiając dane na początku wektory bez zmian.

a) Wektory iii = (1,4,-2), S₂ = (2,-1,-1) uzupełniamy do bazy przestrzeni E³ np o wektor u₃ = (0.0,1). Stosując metodę Grama-Schmidta znajdujemy brakujący wektor

(*3,Pi)a _ (*1;

\Vi\²    ’

**) = _ --- 1’2 =

(i 1 1)

\7'14*14/

Trzynasty tydzień - przykłady

12i

Zauważmy, żc w tym przykładzie wektor t'3 można wyznaczyć także ze wzoru = ti x £? = (—6 —3, -9) lub też przyjąć £3 = (o, 6, c) i rozwiązać układ równań a + 46— 2c = 0,

2a - b - c = 0.

b) Spośród wektorów bazy standardowej przestrzeni E^K dobieramy dwa wektory stanowiące wraz z danymi vi = (1,1,1,0), $2 = (0,1,—1,1) bazę tej przestrzeni. Wektory e₃ = (0,0,1,0), e₄ = (0,0,0,1) są tu dobre, bowiem

1    1    10

0 1-11 0    0    10

0    0    0 1

= 1*0.

Dalsze wektory t'3, Vą bazy ortogonalnej obliczamy ze wzoru

^V3 = *3 -    -~.T

l*l|

(Vi) _    (e_a,v₂),

-----------j-V₇

l*2|

= (0,0, ..o)-l (1,1,1.0) +1(0,1.-1, i) = (-1.0. i. 1) ,

-    (««.**)-    («<> *3)

vą = e*---    ;■ t>i--- :r ^--. „• -w—

l^il

1**1

l^3|

= (0_>0.0.1)-0-i(0,l,-l,l)-l(-io,l.I) = (I,-i,0,I)

r.) Wektor g, = 2z-f 1 uzupełniamy do bazy przestrzeni /?2[r] o wektory p₃ = 1, p₃ = i². Stosując wzory Grama-Schmidta obliczamy brakujące wektory g₂, q₃ bazy ortogonalnej:

^{ft = 1}-I^TIF^{(2t + 1) = 1}-i^{(2l + 1) =} -r ⁺ i

q₃ = x²,

bowiem (p₃, q,) = (p₃. q₂) = ⁰ • Przykład 13.5

Znaleźć bazy ortonormalne podanych przestrzeni euklidesowych i podać współrzędne wskazanych wektorów w tych bazach:

a)    Z= {l>,y,z,l)e£⁴ : 4r - * = 2y - 3*-^ 2! = 0}, 5 = (1,-3,4,9);

b)    E = R2[z] z iloczynem skalarnym zdefiniowanym wzorem

Rozwiązanie

Najpierw wyznaczymy zwykłe bazy rozważanych przestrzeni liniowych, a następnie zor-togonalizujemy je i unormujemy. Współrzędne wektorów będziemy obliczać jak w Przykładzie 13.1. a) Zauważmy, że

E = {(x,y,4x, 6r — y) : z, y € .fi} = lin ((1,0,4,6), (0,1,0, -1)} .