128 129 (3)

Przestrzenie euklidesowc

Bazę przestrzeni E stanowią więc wektory uy = (0,1,0, —1) u? — (1,0,4,6). Fo ich zartogonalizowaniu otrzymujemy bazę ortogonalną 5i =    = (1,3,4, 3), a po unor

mowaniu szukaną bazę ortonormalną

Współrzędne [cri.oj) danego wektora v w tej bazie wynoszą a-. = (t;, e_;) = — 6s/2, *2 = (€, e₂) = v^/35-

b) Będziemy ortogonalizować bazę standardową {],z,z²} przestrzeni K2M Wektory bazy ortogonalnej obliczamy zc wzorów:

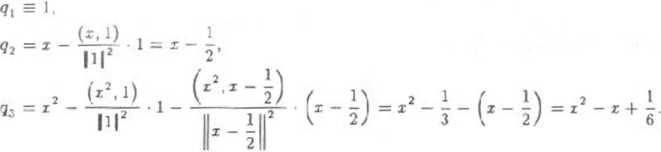
^{li l5}’i^{2 =} n

|    1 = —, więc baza ortonormalna rozważanej

60

Dalej marny |ę Y

przestrzeni składa się z wielomianów rj = 1, r₂ = V3\2x — l), r* = 6>/5 (z² — x +

k    6 /

Wielomian p_c ma w tej bazie współrzędne Oj = (p₀,ri) = o₂ = (p_c> ^rz) = —

2 6

o-a — [p_0t r$) = 0 Zauważmy jeszcze, że gdyby dany wektor p₀ przyjąć jako pierwszy w ortogonalizowancj bazie, to te współrzędne byłyby równe [1,0,0].

• Przykład* 13.6

Zortogonaiizować metodą macierzową podane wektory w odpowiednich przestrzeniach euklidesowych:

a)    i*! = (1,4,2), u? = (1,5,1), w przestrzeni E²\

b)    u\ = (0,1,0.1), w₂ = (-2,3,0,1). U3 = (1,1,1,5) w przestrzeni E*.

Rozwiązanie

a) Niech A oznacza macierz, której wierszami są dane, liniowo niezależne wektory. Stosując operacje elementarne na wierszach macierzy blokowej [,4/4^T|ył]_J bez zmiany ich kolejności, doprowadzimy ją dc postaci [G\A']_t gdzie G jest macierzą trójkątną górną. Wektory wierszowe macierzy A' będą wtedy poszukiwanymi wektorami ortogonalnymi Mamy zatem

I^M] = “

r 21	23 ll 4 2]	*-2 -	21	23	1	4	2
23	27 1 5 1		0	38	2	33	25
L				21	21	21	21

= [GM1

( — 2 33 —25\

—,    ) . Ortogonalizacja Gra

ma Schmidta doprowadziłaby w tym przykładzie do identycznego wyniku.

Trzynasty tydzień - przykłady    ... -...    ... 129 b) Tutaj otrzymujemy

2	1	5	0	1	0	1 '
4	J 4	5	-2	3	0	1
. 6	6	28	1	1	1	5 .

w'3 + **2

2 4    6

0 6-6 0 0    4

“•“2 - 2u-j

*“3 ~ ^3u'l

1 0 1 1 0 -1 -1 1 1

2 16 0 10 1'

[aa^t\a]

0    5-6-2    10-1

0 -6 10 1 -2 0 2 .

= [G\A'].

Po oitogonalizacji uzyskaliśmy więc wektory (0.1,0,1), (-2,1,0,— 1), (-1,-1,1,1). Zauważmy dodatkowo, że kwadraty norm tych wektorów są równe kolejnym elementom głównej przekątnej macierzy G Jest to w tej metodzie ogólna prawidłowość, o ile w trakcie postępowania nie jest wykonywana operacja dzielenia wiersza przez ustaloną liczbę Warto też wspomnieć, że ogólne wzory na ortogonalizację Grama-Schmidta doprowadzi-łyby tu do wektorów (0, 1,0,1), ( — 2,1,0 —1), ( —    — - 1, — |

# Przykład* 13.7

Stosując wyznacznikową metodę skonstruować bazy ortogonalne podanych przestrzeni euklidesowych zawierające dane wektory ortogonalne:

a)    tJi = (2,3,4) w przestrzeni E³\

b)    Ci = (1,1,1,2), V2 = (2, 1, — 1, -1) w przestrzeni E⁴\

c)    ę, = x² — z w przestrzeni f?3[z] z bazą ortonormalr.ą {l.r.z², z³}

Rozwiązanie

Wykorzystamy wyznacznikowy w2Ór na wektor ortogonalny do danych n - I wektorów w przestrzeni eukiidesowej E wymiaru n. Wektor w ortogonalny do wektorów ii i, u?, .... itr.-: € E ma postać

h	h	€n
Oj:	a,2	“In
O n— 1 ]	On-12 •	O n—1 n _

gdzie (o-.i, q,2 .. , Om) oznaczają współrzędne wektora i,, 1 ^ i ^ n — 1, w bazie ortonormalnej { fij, ?2, .., e„} przestrzeni E. Obliczając kolejne wyznaczniki znajdziemy colejne brakujące wektory ba2 ortogonalnych. Początkowa liczbowe wiersze pierwszego wyznacznika będą zawierały współrzędne danych wektorów bazy ortogonalnej w pewnej bazie ortonormalnej. Pozostałe wiersze dopisujemy tak, aby wszytskie liczbowe wiersze były liniowo niezależne. Dla wygody obliczeń będą to wiersze jednostkowe (jedynka i reszta zer). Kolejne obliczane wyznaczniki będą się różnić jednym wierszem - w miejsce pierwszego wiersza dopisanego wstawimy współrzędne nowo znalezionego wektora ba2y.

a) Wektory i, j, k przyjmujemy jako bazę ortonormalną przestrzeni E² Wektor tb = (2,3,4) uzupełnimy o niezależny z nim wektor jednostkowy (0,0,1) otrzymując

«a =	7 j k 2 3 4	= (3, -2,0), v2 =	t j k 2 3 4
	0 0 1		3-2 0

(8,12,-13).