176

gdzie si i r₂ oznaczają pierwiastki równania

«rj² + (ó₁ + ó₂)i+ó_łó₂ = 0.

Wartości chwilowe prądów w uzwojeniach transformatora, wyznaczamy na podstawie relacji podanych w tabl. D.l bądź przez zastosowanie twierdzenia o rozkładzie. Po wykonaniu przekształceń mamy zatem:

gdzie A oznacza wyróżnik równania kwadratowego względem s, które zpstało poprzednio przedstawione. Po podstawieniu wartości danych otrzymujemy

i₂(t) = 10(0,250e^-o,2Sr+0,750e~^1,25r) A, i₂(t) = 10 (e^-0,25t—e~^1,25r) A.

4.28. W obwodzie przedstawionym na rysunku w chwili t — 0 zostaje zamknięty wyłącznik. Przyjmując, że napięcie kondensatora w chwili i = 0 wynosi U₀, a parametry uzwojeń transformatora są znane, określić warunek powstania przebiegów okresowych w obwodzie po zamknięciu wyłącznika i w takim przypadku wyznaczyć wartości prądów w uzwojeniach transformatora.

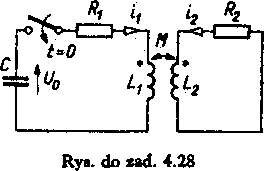
Rozwiązanie. Przyjmujemy oznaczenia

n r . n r L    R₂R₂C Ą-L₂    , / R₂ ~₂

a — R_lL₂+R₂L_l, b--2Ca ’    ⁰⁾⁰ ^ y ■ Ca ~^ ’

Warunek powstania drgań ma postać:

R₂R₂-2R₂y^<%-< R₂R₂+2R₂-^Ą-.

Wartości chwilowe prądów przy spełnieniu powyższego warunku wynoszą

i'i * - —    - |z,₂ cosftło t +    (2R₂CL_t + i?₂ CL₂ - L₂) sin cu₀tj,

MU₀ J _t b .    \

t₂ =-e Mcoscoot--sinft)₀/|.

a    \    a>₀    I

4.29. W obwodzie przedstawionym na rys, a przed zamknięciem wyłącznika panował stan ustalony. W chwili osiągnięcia przez prąd wartości maksymalnej zamknięto wyłącznik. Wyznaczyć wartości chwilowe prądów po zamknięciu wyłącznika, jeśli e = 20sin(500Qt + y) V, R₂ = 6 Q, R₂ = 8 Q, L_x = 1,6 mH, L₂ =■ 8mH.

176