159

Rozwią**nie.Dla t <0 obwód przedstawia się jako obwód jednooczkowy o rezystancji R - R_t+R₂ -5 0, indukcyjności L -0,0318 H i pojemności C -

318 iłF .

CiCa

954-477 954 +477

' Prąd w obwodzie wynosi

i(t) =    sin(«r+We~ <P%

gdzie

\Z\ - VR*+X* - ]/IP + (®L- -^j² - |/5^ł + (10-10)^ł - 5 O,

X

tgq> » — = 0, ę> - 0.

Stąd

»(*) - sin(314f—w/3) - 28,2sin(3l4* - tc/3) A.

Warunki początkowe obliczamy jak następuje

*2.(0-) - i(0-) - 28,2sin(-7r/3) - 28,2(-0,866) - -24,4 A.

«ci(t) - Aci|/*|sin(o)/+y,-«/2) =

~ 314.954.10-^    -

- ,*■    • 28,2«in(314(-57t;6) - 94nin(3141-57i/6) V.

«ci(0“) = 94sin( —§w) * -94-0,5 - -47 V,

Uęzifi * Ac2|/*|sin(a>t+y)|—ti/2) =

* 3ią. 477. jo^-* ‘ 28,2sin(314t—7t/3 — it/2) —

- jjy • 28,2sin(314f- |tc) - 188sin(314f - §*) V, «ci(0") - 188sin( —frt) - -188 - 0,5 - -94 V.

METODA OPERATOROWA

4.8. W obwodzie przedstawionym na rysunku parametry elementów wynoszą odpowiednio: U- 4 V, L_x - 1 H, L₂ - 3 H, R_t - 2 O, i?_a - 4 O. Przed zamknięciem wyłącznika przebiegi były ustalone. Wyznaczyć prąd w oporniku R₂ po zamknięciu wyłącznika.

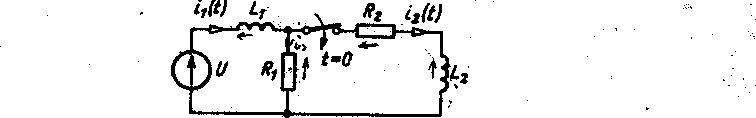
Rys. do sad. 4.8

lSf.