CCF20090408003

Analityczny opis sieci przestrzennych

3.A.Rybarczk-Pirek    1

Sieć jednowymiarowa

Jeżeli punkt P podany zostaje translacji a (o długości wektora |a|) w kierunku osi X, to w wyniku tej operacji powstanie szereg punktów leżących wzdłuż jednej prostej, przy czym odległości między dwoma sąsiednimi punktami będą takie same.

Powstały zespół punktów (węzłów) nazywany jest siecią jednowymiarową (sieć jest przestrzenią nieciągłą) Odcinek między dwoma sąsiadującymi punktami zwany będzie periodem identyczności sieci

Położenie węzłów na osi X określa równanie: x = u a gdzie u jest liczbą całkowitą, a

~a~    o    a długością periodu identyczności

•-•-•-•-•-•-•-•-•

X

3. A.Rybarczyk-Pirek    2

Sieć dwuwymiarowa
Sieć dwuwymiarowa powstaje na skutek działania dwóch różnych translacji ~a i o kierunkach nierównoległych	Siecią dwuwymiarową jest zbiór punktów na płaszczyźnie, których współrzędne x i y spełniają następujące warunki: x = a u
• • T • • • • • —*■ Y	y = 6v
• • • f • •-► a /••/••• / • • / • • • ¥ • • • • X / • •	a, b- periody identyczności sieci w kierunkach X i Y u,v- liczby całkowite
2. A.Rybarczyk-Pirek 3

Sieć przestrzenna (trójwymiarowa)

Siecią przestrzenną jest zbiór punktów (węzłów sieci) w przestrzeni trójwymiarowej, powstający na skutek działania trzech różnych translacji a b c o kierunkach niekoplanamych i nierównoległych (dla żadnej pary translacji)

Współrzędne węzłów sieci przestrzennej w układzie współrzędnych

XYZ spełniają następujące warunki: i

x- a u;y= bv; z =cw

a, b, c - periody identyc23iości sieci

(stałe sieciowe) u, v, w - liczby całkowite

w krystalografii stosowany jest układ prawoskrętny - przejście od osi +X do osi +Y obserwowane z osi +Z wiąże się z wykonaniem ruchu przeciwnego do ruchu wskazówek zegara

3. A.Rybarczyk-Pirek

Wskaźniki węzłów sieci przestrzennej

Położenie węzła w sieci przedstawiane jest za pomocą wektora r o współrzędnych r (uvw) = us + vł + wc

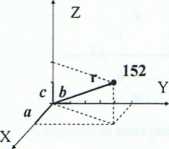
a, b, c- długości odpowiednich periodów identyczności u, v, w - liczby całkowite; wskaźniki węzła

3. A.Rybarczyk-Pirek

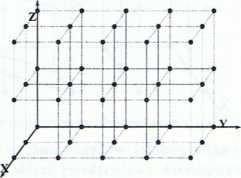
Proste sieciowe

Prosta sieciowa to prosta przechodząca przez co najmniej dwa węzły sieci. Proste sieciowe są skierowane (mają określony kierunek).

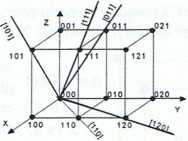
W sieci można wskazać serie prostych sieciowych równoległych do siebie - będą one opisane tym samym kierunkiem.

Kierunek serii równoległych prostych sieciowych podaje symbol («wj. Wynika on ze wskaźników pierwszego węzła uwv przez który przechodzi prosta zawierająca początek układu.

Wskaźniki [uvw] to liczby całkowite i pierwsze względem siebie

3. A.Rybarczyk-Pirek    6