CCF20090516004

Ograniczenia krotności osi obrotu w sieci przestrzennej wynikające z zachowania zasady translacji

Niech będą dane 2 węzły sieci A i B leżące na prostej sieciowej zgodnej z kierunkiem X, odległe od siebie o odcinek długości periodu identyczności a.

Niech przez węzeł A sieci przechodzi oś obrotu o kąt a. Na skutek obrotu węzła B wokół tej osi musi pojawić się węzeł C. Ze względu na periodyczność sieci oś taka przechodzić będzie również przez węzeł B, a na skutek obrotu wokół niej musi pojawić się węzeł D

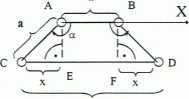
pa

Odcinek CD jest równoległy do    _ ^

odcinka AB. zatem jego długość musi ^P być wielokrotnością długości AB

5. A.Ryt»rczyk-Pirek

AB = a CD = pa = a + 2x; p s C x/a = sin (a-90) = cos a => x = a cosa pa = a + 2(a cosa)

=> cosa = ( p - 1 y 2

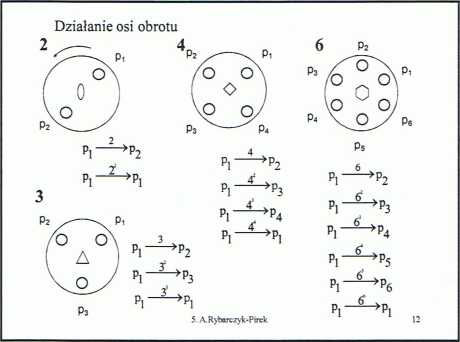
Ze względu na symetrię translacyjną sieci krystalicznej

w krystalografii dopuszczalne są jedynie takie obroty, które umożliwiają szczelne zapełnienie płaszczyzny prostopadłej do osi obrotu. Warunek ten spełniony jest jedynie dla figur o o symetrii dwu-, trój-, cztero- i sześciokrotnej

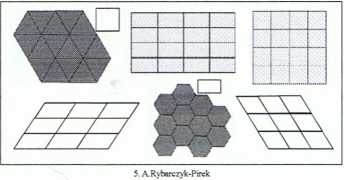
9

UWAGA: możliwe są również obroty o kąt będący wielokrotnością a. W zapisie uwzględnia się wielokrotność => n^k. choć symbol elementu symetrii (pisany i graficzny) pozostaje niezmieniony

Operacje symetrii						Elementy symetrii
l a = 360°						*	tożsamość
2 a = 180°	2^2 2a = 360°					2	0
3 a = 120°	3^2 2a = 240°	3^3 3a =360°				3	A
4 a = 90°	4^2 2a= 180°	4^3 3a = 270°	4^4 4a = 360°			4	O
6 a = 60°	6^2 2a= 120°	6^? 3a= 180°	6^4 4a = 240°	6^5 4a = 300°	6^6 4a = 360°	6	O

Element symetrii może być związany z więcej niż jedną operację symetrii!

5. A-Rybarczyk-Pirck    11

Z rozważań wynika => cosa = (p-l ) / 2, gdzie p e C Funkcja cosinus przyjmuje wartości w przedziale: COSa € <-l; 1>

p	cosa	^a D krotność osi
-1	-1	180	2
0	-1/2	120	3
1	0	90	4
2	1/2	60	6
3	1	0	1

-1 <cosa <1 -1 <(p-l)/2 <1 -2 <p-l <2 -1 <p <3 i p € C

n = 360°/ a

Symbol krystalograficzny n :    1 (a = 360°) 2 (a = 180°)

3 (a =120°) 4 (a = 90°)

6 (a = 60°)

(wg Schoenfliesa C_n C, C₂ C₃ C₄ C₆)

5. A- Ryberczyk-Pirek    8

Symetria obrotowa pięciokrotna, siedmiokrotna, ośmiokrotna itd. w krystalografii jest zabroniona

(niezgodna z sy metrią translacyjną sieci przestrzennej)

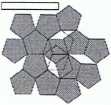
ferrocen

Cząsteczki związków chemicznych i inne skończone obiekty mogą wykazywać symetrię pięcio-, siedmio- czy ośmiokrotną, sieć przestrzenna - NIE !

5. A.R\barczyk-Pirek

10

2