CCF20110602004

r gdy spłacamy w różnych ratach i różnych odstępach czasu Aj, = K.r, + A',r.r, + A .r.r.r. +...+ A r,r,...r

0    II    2 12    3 I 2 3    ii I 2 ii

r gdy spłacamy w równych ratach i różnych odstępach czasu Aj, = Ar, + Ar/, + Ar, Vi +-+A>,r₂...r r gdy spłacamy w różnych ratach i w takich samych odstępach czasu A₀ = Ajr + A,r² + Ajr^J + ... + Kr" r- gdy spłacamy w równych ratach i w równych odstępach czasu Aj, = Ar + Ar^: + Ar * +... + Ar" = A (r + r² + r¹ +... + r")

korzystając ze wzoru na sumę // początkowych wyrazów ciągu geometrycznego tę zależność możemy zapisać w postaci :

Aj, = A

f'^(
k	-r

W powyższych zależnościach wprowadzono następujące oznaczenia:

A„

- kwota bieżąca czyli wartość kredytu:

A, A,, A₂, A₃,..., A„ - raty' umorzeniowe;

(1r^j    - stopa dyskontowa czyli odwrotność czy nnika oprocentowującego s

K-K

r =

s = 1 +

A ■ 100

, gdzie p to roczna stopa procentowa, A - to liczba kapitalizacji w ciągu roku;

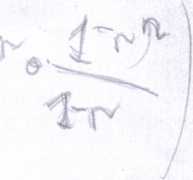
r,,r₂,r₃,...,r - stopy dyskontowe w okresach poprzedzających pierwszą, drugą, trzecią, ogólnie //-tą ratę.

16. Spłacanie kredytu. Warunki spłacania kredytu jednoznacznie określa umowa kredytowa. W niej zawarty jest plan spłaty, wartość stopy procentowej, wysokość prowizji pobieranej przez bank itd.. Generalnie należy podkreślić, że dla banku pieniądz jest towarem, który chcą dobrze sprzedać. Dlatego też zawsze żądają od nas w pierwszej kolejności spłaty odsetek, czyli swojego zysku . a później spłaty kapitału. W szczególności jesteśmy zainteresowani wielkościami rat umorzeniowych i w jaki sposób są one obliczane. Omówimy ten problem na przykładach. PRZYKŁAD 1

W banku A udzielono kredytu w wysokości IQOOO zl, oprocentowanego w wysokości 24% w skali roku. Zgodnie z umową kredyt ma być spłacony w ciągu czterech lat w następujący sposób: po dwóch latach — należnej kwoty.

3    1

po trzech — , a po czterech — należnej kwoty. Wyznacz wartości poszczególnych rat umorzeniowy ch. $    2

Rozwiązanie

^    i

-- -/! i¹

t • !©°

ę^>0 b

Niech A oznacza należną kwotę. Stopa procentowa 24% daje czynnik dyskontujący r = 0,806451612 . Korzystamy ze wzoru Aj, = Ajr + A,r² + A/'+...+ Aj/"    y *    ^ ^ j.

10000 =-A r² +- A r³ +-A r^J stad A = 20430.47 zł.

8 8 2

Ody. Szukane raty umorzeniowe wynoszą: A, = 2553,81 zł. Aj, = 7661.43 zł. Aj, = 10215,23 zł.

PRZYKŁAD 2

W banku B zaciągnięto kredyt w wysokości 10.000 zł oprocentowany na 24% w' skali roku. Umówiono się , że kredyt będzie spłacony w czterech ratach po każdym kwartale, przy czym trzy pierwsze raty będą równe . a ostatnia będzie w' wysokości 50.00zł oraz odsetki będą spłacane w pierwszej kolejności przed kapitałem. Oblicz wartość każdej z trzech pierwszych rat.

Rozwiązanie

Niech szukane pierwsze trzy raty wy noszą A. Stopa procentowa 24% daje czynnik dyskontujący wzgl. jednego kwartału r = 0,943396226 .

Korzystamy ze wzoru A_ft = Aj/- + A₂r² + A ,/* +... + Aj/"

10000 = A • r + A • /-² + A • r ' + 5000 • r⁴ stąd A = 2259,45 zł Odp. Szukane raty umorzeniowe wynoszą Aj = Aj = Aj = 2259,45zł Aj = 5000zl PRZYKŁAD 3

W banku C zaciągnięto kredyt w wysokości 10.000 zl oprocentowany na 24% w skali roku. przy czym zrezygnowano z kapitalizacji odsetek Umówiono się . że kredyt będzie spłacony w czterech kolejnych ratach płatnych na koniec każdego kwartału w następujących wysokościach: po I kwartale 500zl. po II kwartale 2000zł, po III kwartale 8000, a po IV kwartale resztę należnej kwoty. Oblicz wysokość ostatniej raty jeśli zgodnie z umową, z kolejnych rat