Ek Matematyczna Materia³y 4 4

Modele pokrewne

Omawiany model pajęczynowy M. Ezekiela (1938) możemy zapisać tak:

P^E(t) =    p(t-1),

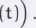
p(t) = v(v^E

Oczekiwania cenowe (pierwsze z równań) są naiwne.

Model oczekiwań ekstrapolacyjnych R. M. Goodwina

(1947)

j P^E(t) = p(t — 1) + p(p(t — 1)—p(t — 2)), | p(t) = P(p^E(t)).

Oczekiwania cenowe sÄ… ekstrapolacyjne, p — współczynnik oczekiwaÅ„; ustalona liczba, p = 0 opisuje naiwne oczekiwania, p > 0 zmiany w tym samym kierunku, co poprzednio, a p < 0 zmiany w przeciwnym kierunku.

Model oczekiwań adaptacyjnych M. Nerlove’a (1958):

P^E(t) = p^E(t-1)+ri(p(t-1)-p^E(t-1)), P(t) = ^(p^E(t))-

Oczekiwania cenowe sÄ… adaptacyjne, p — współczynnik dostosowania oczekiwaÅ„ (adaptacyjnych); ustalona liczba, zwykle 0 < p sj 1.

K. M. Przyłuski dla Studentek i Studentów WSE-I

X.2005

Dynamika 9