klugi sciagi3

dVx SVy 3Vz

= 0

Różniczkowe równania Eulera stosuje się zarówno dia mchu potencjalnego, jak i wirowego. Dla ruchu wirowego można wydzielić składowe prędkości kątowej co. Przekształcając pochodną prędkości

dVx przy wykorzystaniu zależności

1 (dVi	3Kv'
2(ą.

1'

2\dz    8x J

2 ^ dx    dy )

otrzymuje się 8V.r BVx „ 5Vx

dV_r t K SK _{ J dK    _[ y OK

♦p/SŁ-Ąk*1=

V Sz Stc J dx

₌    +K- +yr)-2y>a,:-2Ka,.

dl 2 dx    '

wyrażenie w nawiasie jest iloczynem skalarnym v-v = v'

22. PRZEDSTAWIĆ RÓWNANIE BERNOULLIEGO DLA PŁYNU DOSKONAŁEGO

Przyjmując pewne założenia, można scalkować różniczkowe równania mchu płynu nielekkiego. Poniżej zostały podane dwa takie rozwiązania. Pierwsze rozwiązanie zostanie wyprowadzone przy założeniach:

-    mch jest ustalony.

-    płyn jest barotropowy (gęstość płynu zależy tylko od ciśnienia),

-    siły masowe mają potencjał, który będzie oznaczony przez - U.

Mnożąc skalarnie wszystkie składniki równania Eulera przez przesunięcia elementu po jego torze ds. = vdt. otrzymuje się

dv    1

--ds = Fja> • ds--gradp ds

dt    p

Wyrażenie po lewej stronie równania można przekształcić do postaci

I ^av i dv    \ v¹

|--ds =--\>dt = dv- v = d\ —

|    dt dt    {2 _y

! Ponieważ składowe jednostkowych sil masom ch m-KOsza

dU _z_ 3U

dy    dz

więc rozpisując drugi iloczyn skalamy równania, otrzymuje się

_ , (su . su . su A ...

Pj.-I -    = — -(IX* -r —7- (IV H—— </z i - -au

^ dx dy ' oz j

Trzeci iloczyn skalamy równania można zapisać w postaci

1    . _J 1 (Sp . dp . dp A 1 _J

--gradp-01 =---7-    i/A*-rdy+ — ar 1=--dp^-dP

P    p\dx    dy    oz    j p

gazie p _ r^P_

P

os ta lecznic o irzy mujenty

całkowanie tego równania wykonuje się wzdłuż toru

u = gi

T⁺^7^=c

T⁺^T=^C

V    p

_{T +} £r + - =

L    O

2g

- = const.

23. PRZEPŁYW UWARSTWIONY PŁYNU RZECZYWISTEGO - PROFIL PRĘDKOŚCI I RÓWNANIE HAGENA - POISEUILLE'A Rozpatruje się ustalony przepływ płynu nieściśliwego w przewodzie kołowym o promieniu R. Tor>' elementów płynu są liniami prostymi, równoległymi do osi x. będącej osią pizew-odu. W rozważanych warunkach składowe prędkości V>-oraz Vł są równe zeru. Po pominięciu wpływu sil masowych [x * Y * Z « O) * ^lrzY równania Naviera - Slokesa i równanie ciągłości uproszczą się do postaci

cY,___1 dp , / d-V* , d²K- , c-V<

dx    p dx i ar" dy² dz³

o ^1Sd	31. WYJAŚNIĆ POJĘCIA STRAT
	LOKALNYCH, PODAĆ PRZYKŁADY
p oz	Podczas przepływu mogą wvslapić lokalne
0- ^iBp	zaburzenia wywołane zmianą kierunku ruchu.
u cy	gwałtownym rozszerzeniem bądź zwężeniem, dzieleniem lub łączeniem sic strumieni.
^ = 0	Zaburzenia tc rozpraszają część energii
dx	strumienia, co ujawnia się w postaci strat

Równanie drugie i trzecie układu wskazują, żc ciśnienie jest funkcją tylko współrzędnej x. Z czwartego równania (ciągłości) wynika, że prędkość V* zależy wyłącznie od y i z. Z lego względu pierwsze równanie można zapisać w postaci

5-v_x t d²r*) dp

#*t)

dx

Ponieważ lewa strona równania jest funkcją y i z. a prawa tylko x, więc wynika stąd. żc równanie może być spełnione, gdy obie strony są wielkościami stałymi

d*V* d^zV.^ _ 1 dp _Ap =”^{2 +} dz¹

= const.

óy* dz" J u dx pL gdzie Ap oznacza różnicę ciśnień powstałą na długości L przewodu. Równanie będzie rozwiązane dla warunku brzegowego, brzegowego którym prędkość V* przy ściance przewodu (r=R). wskutek adhezji jest równe zeru.

r = R=>V_x = 0

Łatwo można wykazać, że równanie Stała C przyjmuje wartość

r--^L

4pL

Po wykonaniu podstawień funkcja prędkości przybiera posiać

ki = -

'4 pi. '

R‘)

Otrzymane równanie dowodzi, że dla przyjętych warunków ruchu, rozkład prędkości w przekroju poprzecznym przewodu kołowego jest parabołoidalny. Elementarny wydatek płynu dQ przez powierzchnię pierścienia dA poprzecznego przekroju przewodu kołowego jest równy

dO = VxdA = Vx2jirdr Objętościowe natężenie przepływu płynu Q w przedziale wynosi

O = 2zkrdr =    - Ądr = -Ą

o    2fiLV ’    3 pL

Równanie (o nosi nazwę równania Hagena -PojseuiIle’a 24

miejscowych.

Wysokość strat ciśnienia przy przepływie płynu przez przeszkody lokalne oblicza się ze wzoru

hm=Ai=ę i—

r    2 g

gdzie ę - współczynnik oporu miejscowego. Współczynnik Czależy od: rodzaju przeszkody (np. zawór, kolano), parametrów geomctiycznych charakteryzujących daną przeszkodę (stopień otwarcia zaworu, promień krzywizny i kąt zmiany kierunku przepływu w kolanie), a także od liczby Reynoldsa.

32. OBLICZANIE POJEDYNCZYCH PRZEWODÓW KRÓTKICH

W przewodach krótkich straty miejscowe są na tyle duże w stosunku do łącznych strat ciśnienia, żc nie mogą być pominięte w obliczeniach hydraulicznych.

Obliczenia hydrauliczne pojedynczych przewodów można sprowadzić do trzech podstawowych wariantów, obejmujących wyznaczenie strat hydraulicznych li*, wydatku cieczy Q oraz doboru średnicy przewodu D. Na rysunku zaznaczono przekroje I i 2. dla których układa się równanie Bcmoulliego. Symbolem p.p. został oznaczony poziom porównawczy, względem którego odnosi się wysokości energii w obu przekrojach. Zakłada sic. żc przekrój zbiornika (1) jest wielokrotnie większy od przekroju przewodu <Ai »A2), a nich cieczy w przewodzie jest ciągły i ustalony (Q = const) rysunek

W celu obliczenia strat hydraulicznych lu powstałych pomiędzy przekrojami I i 2 należy

jego chropowatość bezwzględna k* współczynniki oporów* miejscowych gj oraz wydatek cieczy Q. Wysokość strat ciśnienia lu jest równa sumie strat liniowych Ul i strat powstałych na oporach miejscowych hm. Dla przyjętego schematu straty te wynoszą

O 2g 5* 2g [ 'O “1*/ 2g

Z równania ciągłości oblicza się średnią prędkość przepływu cieczy w przewodzie ^ _ Q Al

W celu określenia współczynnika oprów liniowych należy obliczyć liczbę Reynoldsa _ ViD oraz chropowatość względną _ k v    ^ ~~D

a następnie z nomogramu Coicbrooka - Wlutc a wyznaczyć współczynnik Układając równanie Bernoullicgo dla przekrojów 1 i 2

PrI ₊ CC\V\^Z ^ p*i ^ aiVi² ^

Y

Y

można obliczyć np. wskazania manometru p»z. Dla

pii=0, Ai» /f2 => Ki = 0, ai = cci = 0

otrzymuje sic

-h.\_r

^P"~    ^2g

gdzie a- różnica wysokości między przekrojami. W celu obliczenia wydatku cieczy Q zakłada się, że znane są: wymioty geojnctry-cznc (D. L) i chropowatość k przewodu, wskazanie manometru pał wysokość a, jak również opon^- miejscowe. 2 przekształcenia równania Brcnoulliego otrzymujemy

. L , 4, .

a.—i+y

o ź*

Ponieważ nic jest znana w artość Rc. nic jest więc możliwe obliczenie współczynnika ż (Re. o) W tym przypadku należ)- zastosować metodę kolejnych przybliżeń (iteracyjną). W pierwszym prz>^rbliżeniu zakłada się. że przepływ' odbywa się w strefie kwadratowej zależności strat.). -Dla odczytanej z nomogramu Coicbrooka -Whitc’a wartości 1 oblicz się V:, liczbę Rc i ponownie odczytuje X. Tok obliczeń kończ)¹ sie z chwilą, gdy różnica dwóch kolejnych wartości X mieści sic w zakresie przyjętej dokładności metody iteracyjnej. Ostatnia wartość prędkości V: pozwala wyznaczyć z równania ciągłości szukany wwdatek

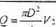
4

W celu określenia średnic)^- przewodu D przyjmuje się. żc znana jest długość przew odu L oraz. dla zadanego wydatku Q. określona jest dyspoz.ycyjna różnica piczomcttycznej iinii ciśnień.

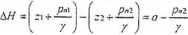
dla warunków zadania otrzymuje się

Przez porównanie AH z obliczonymi wartościami AHi przyjmuje się jako rozwiązanie zadania taką średnicę katalogową ( średnicę nominalną, lub wewnętrzną), dla której AH. jest równe lub nieznacznie mniejsze od dyspozycyjnej różnicy AH.

33. LINIE PIEZOMETRYCZNE ł ENERGII

Dla zanalizowania pracy' rurociągu, wskazania miejsc, gdzie może wystąpić kawitacja, określenia obciążeń warunkujących wytrzymałość konstrukcji, sporządza się wykres ciśnienia w zależności od współrzędnej liniowej mierzonej wzdłuż osi rurociągu. Na tym wykresie odkłada się zmiany ciśnienia wywołane zmianą wysokości położenia osi rurociągu i zmianą średniej prędkości, spadki ciśnienia spowodowane wszelkimi stratami i przyrosły ciśnienia wywołane pracą pomp.

Wszelkie le wielkości łatwo jest obliczyć z równania Bernoullicgo obejmującego straty i dostarczenie energii przez pompy. Dla przepływów cieczy stosujemy często określanie ciśnienia w jednostkach wysokości słupa cieczy przepływającej rurociągiem, wtedy rzędne na wykresie mają wymiar liniowy. Rzędne te odpowiadają wysokościom slupów cieczy w otwartych rurkach pionowych, które możemy przyłączyć do przew odu wc wszystkich interesujących punktach. Takie rurki do pomiaru ciśnienia ( nadciśnienia ) nazywa się piezometriami. Stad też wykres ciśnień wyrażony w jednostkach wysokości słupa cieczy, której przepływ badamy, nazywamy wykresem piezomet tycznym (linią piczo metryczną). Jeżeli w przcwmdzic występują podciśnienia, rurki piczomcttyczne należałoby zastąpić rurkami w kształcie litery U. Jeżeli w-zdluż wyprostowanej osi rurociągu wykonamy wykres jednostkowego strumienia energii ( mechanicznej), wykres taki nazwiemy w skrócie .. wykresem energii" (linią energii). Na wykresie tym odkłada się tylko straty energii oraz jej przyrost ( pompa).

Na wykresie piczomcttycznym mogą występować wzrosty ciśnienia wywołane powiększeniem przekroju lub obniżeniem osi przewodu, rysunek

Na rysunku przedstawiono wykres piczo metryczny i wykres energii mechanicznej wybranego przewodu. Jeżeli sporządzimy wykres energii mechanicznej idąc od obydwu końców^- przewodu aż do pompy, to odcinek zamykający określi niezbędną moc pompy. tj. energię, jaką pompa musi dostarczyć cieczy w jednostce czasu.

34. PRZEPŁYW CIECZY PRZEZ LEWAR Lewarem nazywa się przewód umożliwiający przepływ cieczy między zbiornikami, którego oś wznosi się powyżej swobodnego zwierciadła w zbiorniku zasilającym. Warunkiem powstania ruchu w lcw^rarzcjest jego wstępne napełnienie cieczą. Wylot z lewara może być swobodny lub zanurzony w^r zbiorniku dolnym ( odbiorniku), rysunek