logika skrypt 2

22

stadniny — n (nazwa),

janowskiej — — (funktor nazwotwórczy od jednego argumentu nazwowego). n

Zestawienie symboliczne przedstawia się następująco: n

n z    n ' n

n —    — n —.

n    nn    n n

n

7. LOGIKA FORMALNA

7.1.    Logika formalna jest tym działem logiki, który dotyczy schematów rozumowań niezawodnych, to jest takich, które od prawdziwych przesłanek prowadzą zawsze do prawdziwych wniosków. A więc, logika zajmuje się tym szczególnym rodzajem rozumowania, które nazywa się wnioskowaniem. Wnioskowanie bowiem zajmuje bardzo poczesne miejsce w naszym opisie świata, jak również w opisie jego przekształceń.

7.2.    Określenie — formalna — wynika z faktu zajmowania się głównie schematami rozumowania, to znaczy, że przedmiotem zainteresowań nie jest treść zdania a forma, budowa zdania. Jak się bowiem okaże, sama budowa zdania może przebiegać według schematu, który zawsze gwarantuje jego prawdziwość.

7.3.    Należy wyjaśnić, że niektóre schematy zdań prawdziwych dadzą się przedstawić w postaci reguł wnioskowania. Na przykład dzisiaj jest czwartek, zatem jutro jest piątek. Jest to zdanie, które można zapisać w innej postaci: jeśli dzisiaj jest czwartek, to jutro jest piątek i dzisiaj jest czwartek, to jutro jest piątek. W tym drugim przypadku mamy do czynienia z dwiema częściami rozumowania, mianowicie z wiadomościami, które posiadaliśmy przed rozpoczęciem rozumowania oraz z wiadomościami, które wywodzą się z poprzednich drogą pewnego rozumowania.

Jeśli dzisiaj jest czwartek, to jutro jest piątek i dzisiaj jest czwartek — to jest informacja, którą znaliśmy wcześniej. W logice nazywa się onS¹ przesłanką, stanowi bowiem, jeśli można tak powiedzieć, przesłanie części po niej następującej, która nazywa się wnioskiem i w przypadku naszego zdania będzie to wyrażenie: to jutro jest piątek.

7.4.    W formule: poniewai_dzisiaj jest czwartek, to jutro jest piątek: mamy do czynienia ze stosunkiem wnioskowania. W formule np.: Jeśh dzisiaj jest czwartek, to jutro jest piątek mamy do czynienia z wynikaniem czy też implikacją. Wypowiadając taką implikację, nie mówimy nic o tym, czy uznajemy zdanie poprzedzające, czy następne. Natomiast mając do czynienia z wnioskowaniem, stwierdzamy o związku zdania jednego i drugiego.

s

7.5.    Wyróżnić zatem należy schematy formalne zdań i schematy formalne wnioskowań. Schematy formalne uzyskamy wtedy, gdy w zdaniu złożonym występują zdania proste i łączące je spójniki zastępujemy odpowiednimi symbolami. Podobnie należy postępować tworząc schemat zdań kategorycznych. Aby utrzymać składniową jednoznaczność, wprowadzamy nawiasy. I tak, np. przyjmując symbole

zmiennych zdaniowych p, q, r-a, odpowiednie znaki spójników np.: —* implikacje, A koniunkcja, negacja, możemy zdanie typu: jeżeli 7 dzieli się przez 6; to 7 dzieli się przez 2 oraz 7 dzieli się przez 3, zapisać symbolicznie:

p-{qAr)

gdzie: p — 7 dzieli się przez 6, ' q — 7 dzieli się przez 2, r — 7 dzieli się przez 3, łącznik zaś: jeżeli ... to .... oznacza symbol —.

Zdanie: każdy pies jest ssakiem, mogę symbolicznie zapisać w postaci: SaP, gdzie: 5 — pies,

P — ssak.

Mamy tu do czynienia ze zmiennymi nazwowymi.

7.6.    Schematy zdań zawsze prawdziwych nazywamy tautologiami wnioskowania bądź niezawodnymi schematami wnioskowania. Już wspomniano, że może zachodzić tożsamość między tautologią (zwaną niekiedy tezą lub prawem logicznym) a niezawodnym schematem wnioskowania.

Z uwagi powyższej wynika, że niekiedy schemat zdaniowy jest schematem zdania prawdziwego i podobnie jest . ze schematem wnioskowania, np. zdanie: Kościuszko byl Polakiem lub Kościuszko nie był Polakiem, jest zdaniem, którego zapis formalny można przedstawić: pv nie p{pvp) i czytamy p lub nie p. Schemat ten może być schematem zdania tylko prawdziwego.

7.7.    Po tych wstępnych wyjaśnieniach należy wprowadzić kilka podstawowych pojęć.

Logika formalna, jak to było wcześniej powiedziane, posiada kilka ważnych działów, takich jak:    .

—    rachunek zdań,

—    rachunek nazw,

—    rachunek kwantyfikatorów,

—    rachunek relacji,

—    rachunek zbiorów.

7.8.    W niniejszym wykładzie ograniczymy wykład logiki formalnej do elementów rachunku zdań i rachunku nazw nawiązując, o ile to będzie potrzebne, do działów pozostałych.

Celem bowiem tego wykładu nie jest przedstawienie słuchaczom skomplikowanych problemów logiki jako dyscypliny naukowej, ale pomoc w poprawnym formułowaniu własnych myśli, własnych wypowiedzi, najczęściej wygłaszanych w języku naturalnym, w sposób zgodny z zasadami logiki.

Tak więc, trudne zagadnienia formalne, charakterystyczne dla logiki matematycznej, przy danym wymiarze godzin nie mogą być przedmiotem wykładu. Nie to ma na celu niniejszy wykład, zainteresowani zaś mogą korzystać z wykładów logiki prowadzonych przez matematyków.

7.9. Rachunek zdań (logika zdań, teoria zdań, teoria dedukcji) zajmuje się związkami międzyzdaniowymi ujmowanymi w zdania złożone, powstające z łączenia zdań funktatorami zdaniotwórczymi od argumentów zdaniowych. Ponieważ w rachunku zdań nie używa się konkretnych zdań, lecz zmiennych zdaniowych, które reprezentują zdania -dlatego w logice zdań nie mamy do czynienia ze zdaniem, lecz z funkcjami zdaniowymi. Jeżeli zaś w funkcji za zmienne podstawimy stałe, to uzyskamy zdanie w sensie logicznym.

7.10* Język rachunku zdań. W rachunku zdań posługujemy. się stałymi logicznymi, które najczęściej symbolizowane są w sposób następujący:

- lub niekiedy ■ —* lub niekiedy A lub niekiedy

-    negacja, czytamy nieprawda, te .... nie,

-    implikacja — czytamy jeżeli... to,

-    koniunkcja — czytamy i (ale jednocześnie można zaliczyć do koniunkcji wyrażenia typu: oraz, ale, lecz, a, natomiast),

v    — alternatywa prosta — czytamy lub, bądź w sensie

co najmniej jedno z dwojga,

lub niekiedy — alternatywa wyłączająca, zwana niekiedy ek-skluzją, czytamy albo, niekiedy również lub, w sensie dokładnie jedno z dwojga,

I    — dysjunkcja czytamy bądź — bądź, lub w sensie co.

najwyżej jedno z dwojga,

=    — równoważność, czytamy zawsze i tylko wtedy ...

jeżeli, pod tym. warunkiem i tylko pod tym warunkiem, że,

1    — binegacja, czytamy ani... ani

7.11. W rachunku zdań posługujemy się również zmiennymi logicznymi, których symbolem są najczęściej małe łacińskie litery i to tradycyjnie rozpoczynające się od litery p, q, r, s, t, ale można się również spotkać z inną symboliką. Należy wówczas zwracać uwagę czy chodzi o zmienne zdaniowe, czy nazwowe.

7.12. Zmienne zdaniowe stanowią argumenty, niekiedy nazywane czynnikami. Argumenty wraz z funktorami tworzą funkcje zdaniowe, a dokładniej funkcje logiczne, jeżeli funktory przedstawione są w postaci symbolicznej. Przedstawione funktory mogą występować z jednym bądź dwoma argumentami. Ściślej rzecz biorąc,

tylko funktor negacji stanowi funktor jednoargumentowy. Zastępując zmienne zdaniowe i stałe logiczne odpowiednio zdaniami i spójnikami, otrzymamy zdanie właściwe. Funkcje zdaniowe same nie posiadają wartości logicznej, uzyskują je po odpowiednim podstawieniu.

7.13.    Funktory takie określamy w logice mianem funktorów prawdziwościowych, a niekiedy funktorów ekstensjoaalnych. „Mała encyklopedia logiki” określa funktor prawdziwościowy, czyli ekstensjonalny następująco:

„Jeśli wyrażeniem utworzonym przez funktory jest zdanie złożone, a denotacją zdania jest wartość logiczna (prawdziwość łub fałszywość), to funktor jest wówczas ekstensjonalny, gdy wartość logiczna zdania zależy wyłącznie od wartości logicznej zdań składowych a nie zależy np. od ich treści. Taki funktor nazywa się prawdziwościowy (ekstensjonalny) z racji zależności pomiędzy prawdziwością argumentów a prawdziwością całego zdania złożonego”¹.

Zależność wartości logicznej zdania złożonego od wartości logicznej zdań składowych (argumentów) przedstawia się w tzw. matrycach (tablicach rachunku zdań).

Konsekwencje tej formuły sprawiają niekiedy słuchaczom spore trudności. Można się bowiem spotkać z przykładami zdań, które logika formalna uznaje za zdania prawdziwe, a potoczne odczucie nie dostrzega związku wynikania między elementami danego zdania złożonego. Oto przykład podany trafnie przez T. Kotarbińskiego: „Jeśli ptaki mają skrzydła, to niedziela jest dniem świątecznym”². Implikacja taka wyrażona symbolicznie p — q jest prawdziwa z punktu widzenia matrycy implikacji, natomiast nie jest prawdziwa, jeśli użyty spójnik warunkowy rozumieć tak, jak w języku potocznym. Od zdania warunkowego wymaga się potocznie, aby można było słusznie wnioskować następnik z poprzednika. Przykład ten wskazuje na pewne rozbieżności w pojmowaniu spójnika prawdziwościowego w języku potocznym i w logice. Z punktu widzenia logiki te dwa zdania (w przytoczonym przykładzie) dają nam całość, którą z punktu widzenia zasad logiki uznać trzeba za pra w d z i w ą, ponieważ p r a w d z i w o ś ć tej całości zależy li tylko od prawdziwości zdań składowych.

7.14.    Za pomocą zmiennych i stałych logicznych konstruujemy schematy formalne zdań zwane funkcjami logicznymi, a z nich te, które przy każdej wartości argumentów (0,1) (w logice dwuwartościowej) prowadzą do zdania prawdziwego, nazywają się tautologiami, bądź prawami logicznymi, czy też tezami rachunku zdań.

7.15. Oto podstawowe funkcje zdaniowe, czyli wyrażenia złożone z argumentów i funktatorów prawdziwościowych wraz z odpowiednimi matrycami, czyli tabelami. Tabele są zbudowane w ten sposób, że za poszczególne zmienne, w tym przypadku dwie: p i q, podstawiamy wartości 1 lub 0. Wartość całości funkcji zdaniowej jest zasadniczą charakterystyką danego funktora. Stanie się to bardziej zrozumiale, jeżeli przedstawimy konkretne przykłady,

a) Oto zapis symboliczny i tablica implikacji (matryca) p q (czytamy: jeśli p to q).

Tablica implikacji

p	?	p—ą
1	1	1
1	0	0
0	1	1
0	0	1

Rubryka p oznacza wartość logiczną jednej zmiennej zdaniowej (oczywiście w skali 0,1); rubryka q wartość logiczną drugiej zmiennej zdaniowej. Rubryka trzecia — p —q — oznacza wartość całości w związku z wartością części składowych.

Ta część, która występuje jako pierwsza, czyli przed wyrażeniem „to”, nazywa się poprzednik, a część następująca po „to” nazywa się następnik. Zgodnie z tabelą możemy stwierdzić, że implikacja jest zawsze prawdziwa z wyjątkiem, gdy poprzednik jest prawdziwy a następnik fałszywy.

Przy tej okazji należy teraz (choć później będziemy o tym jeszcze mówić) wspomnieć o zależności między związkiem implikacyjnym a związkiem wynikania jednego zdania z drugiego,, czyli związkiem wnioskowania. ■

Te zależności w sposób klarowny wyraża Z. Ziembiński.³ Ze zdania Z_x wynika zdanie Z₂ wtedy i tylko wtedy, gdy:

1)    implikacja zbudowana ze zdania Z_x jako poprzednika i zdania Z₂ jako następnika jest prawdziwa oraz    ,

2)    prawdziwość tej implikacji opiera się na jakimś związku między tym, co głosi zdanie Z_x a tym, co głosi zdanie Z₂.

O charakterze tych związków będzie mowa później.

Warto wspomnieć jeszcze o innej charakterystyce.

Jeżeli z poprzednika implikacji wynika jej następnik, to poprzednik nazywamy racją, a następnik implikacji następstwem,

Racja i następstwo są to dwa człony stosunku zwanego wnioskowaniem. Jeżeli używamy zatem terminu racja i następstwo, to mówimy tylko o zdaniach składowych implikacji prawdziwej i zarazem o odpowiednim charakterze związku między jednym a drugim zdaniem.

b) Funktor koniunkcji w połączeniu z argumentami tworzy funkcję zdaniową

zwaną również koniunkcją; symbolicznie: p a q (czytamy p i q).

Tablica koniunkcji

p	9	PAQ
1	1	1
1	0	0
0	ł	0
0	0	0

Należy pamiętać o tym, że funktor i może również pełnić rolę funktora nazwotwór-czego od dwóch i więcej argumentów nazwowych. W użyciu koniunkcyjnym i występuje w wyrażeniu A jest B i C, w znaczeniu enumeracyjnym A i B to C.

c) Funktor alternatywy prostej (symbol v) tworzy funkcję zwaną alternatywą prostą;

symbolicznie: p v q (czytamy p lub q).

Tablica alternatywy

p		pvq
1	1	1
1	0	1
0	1	1
0	0	0

Możemy się spotkać z symbolem + jako symbolem alternatywy. Jest ona przyrównywana w rachunku zdań do dodawania w matematyce, tak jak koniunkcją jest czasem oznaczana symbolem •, bowiem traktuje się ją na podobieństwo mnożenia.

d) Funktor alternatywy rozłącznej lub wyłączającej tworzy funkcję o tej samej nazwę;

symbolicznie: p * q (czytamy p albo q).

Tablica alternatywy rozłącznej

p	ą	p+q
1	i	0
1	0	1
0	i	1
0	0	0

W języku potocznym często nie odróżnia się funkcji znaczeniowych spójnika lub, albo, bądź. Przykład podany w książce Z. Ziembińskiego może nieco sprawę wyjaśnić, choć dotyczy problemów prawnych. Na przykład według danego przepisu za pewien czyn przestępca powinien być ukarany przynajmniej jedną z dwóch kar przy możliwości wymierzeniu obu na raz, czy też jedną i tylko jedną, czy też co najwyżej jedną. Jeśli sami wystąpilibyśmy w roli oskarżonych, znaczenie słowa lub nie byłoby dla nas obojętne. Czasami lub może wystąpić jako funktor nazwotwórczy, np. uczony lub szarlatan.

e) Funktor dysjunkcji tworzy funkcję dysjunkcji; symbolicznie:- p/q (czytamy bądź p, bądź q) Prawdziwość obu zdań jest warunkiem wystarczającym do uznania fałszywości dysjunkcji.

Tablica dysjunkcji

p	?	p/q
1	1	0
1	0	i
0	1	T
0	0	1

f) Funktor równoważności tworzy funkcję równoważności; symbolicznie: p = q (czytamy: p zawsze i tylko wtedy, gdy q).

Tablica równoważności

p		HI *4
1	i	ł
1	0	0
0	i	0
0	0	1

Przy tworzeniu zdań złożonych z więcej niż dwóch należy stosować nawiasy celem uniknięcia nieporozumień.

Zdania równoważne należy odróżniać od zdań równoznacznych.

g) Funktor negacji tworzy funkcję negacji; symbolicznie: ~p (lub p') (czytamy: nieprawda, że p lub nie p).

Tablica negacji

p	~p
1	0
0	1

Wyrażenie nieprawda jest tak, że, synonimiczne nieprawda, że, języku polskim zaznacza się umieszczeniem partykuły przeczenia przed odpowiednimi czasownikami np. nieprawda, że Jan jest ekonomistą, mówimy Jan nie jest ekonomistą. Należy wyraźnie odróżnić zdania s.prz e_cjzn e od z d a ń przeciwnych. Zdania typu: Szkoła Główna Handłowa została zbudowana przed II wojną światową i nieprawda, że Szkoła Główna Handlowa została zbudowana przed II wojną światową są zdaniami sprzecznymi. W odniesieniu do zdań sprzecznych można sformułować ważne twierdzenia logiczne, nazywane także zasadami myślenia. Są to:

Zasada sprzeczności (symbolicznie: ~ (p a ~p)). Dwa zdania względem siebie sprzeczne nie mogą być zarazem prawdziwe (czytamy: nieprawda, że p i nie p).

Zasada wyłączonego środka, (symbolicznie: pv ~p; czytamy p lub nie p).

Dwa zdania względem siebie sprzeczne nie mogą być oba fałszywe.

Zasada podwójnego przeczenia (symbolicznie: p = ~(~p); czytamy p jest równoważne nieprawda, że nie p).

Zdanie podwójnie zaprzeczone ma wartość logiczną taką samą jak zdanie, które jest niezaprzeczone.

Wymienione trzy zasady nazywane są w logice również podstawowymi prawami myślenia.

Należy odróżnić, jak już zaznaczone, zdania sprzeczne od-zdarrprzeczących. Na przykład para zdań przeczących to: Kwiatkowski jest znakomitym pisarzem i Kwiat-kowsld jest analfabetą. Te zdania mogą być gfeydwa-^rewdstwe-robydwa fałszywe, cofnie może się zdarzyć parze zdań sprzecznych.

h) Funktor binegacji tworzy funkcję binegacji; symbolicznie: p 1 ą (czytamy: ani p ani q).

Tablica binegacji

p	q	p i q
1	. i	0
1	0	0
0	i	0
0	0	i

Funktor binegacji ma tę właściwość, że z jego pomocą można zdefiniować wszystkie pozostałe funktory, podobnie jest z funktorem dysjunkcji.

7.16. Języki naturalne posiadają o wiele więcej spójników prawdziwościowych niż te, o których mówiliśmy. Chodzi bowiem o możliwość bardziej adekwatnego zapisu jakiejś rzeczywistości. Mówimy również o możliwości zdefiniowania jednego spójnika prawdziwościowego za pomocą innego, to znaczy, że zastosowanie w zdaniu spójnika b zamiast spójnika a nie zmieni sensu tego zdania. Powstanie natomiast zdanie równoważne, które danego spójnika nie zawiera..

Na przykład funktor dysjunkcji można zastąpić funktorami negacji i alternatywy':

p/q = ~pv~q.

Na przykład funktor binegacji może być zastąpiony przez negację i koniunkcję: p lq = ~pA~q.

Problem ten nie będzie przedmiotem naszego szczegółowego wywodu, choć należy wiedzieć, że wszystkie spójniki prawdziwościowe są definiowalne za pomocą odpowiednio dobranych zbiorów spójników: np.    I-jY}¹. W związku

i

B. Stanosz: Wprowadzenie do logiki formalnej. PWN, Warszawa 1985, s. 23.

z tym można stwierdzić, że „każdy schemat prawdziwościowy można, korzystając z odpowiednich definicji, »przetłumaczyć« na schemat, w którym występują tylko owe wyróżnione spójniki”⁴.

Ograniczenie do minimum liczby fiinktorów stosuje się przy konstrukcji tzw. aksjo-matycznych systemów rachunku zdań.

7.17.    W zapisach symbolicznych posługujemy się również nawiasami w celu wydzielenia określonych całości syntaktycznych i uniknięcia tym samym nieporozumień.

7.18.    W niektórych przypadkach, np. jeżeli chcemy podkreślić tezowy charakter danej formuły zdaniowej, korzystamy dodatkowo z symboliki rachunku kwantyfika-torów.

7.19.    Rachunek kwantyfikatorów nazywany bywa również rachunkiem predykatów, to jest nazw odnoszących się do własności łub stosunków, np. wyrażenie zapisane symbolicznie:

\x) ^P(x) Q{x)>

czytamy: dla każdego x jeśli P od x to Q od x. Na przykład dla każdego przedmiotu, jeśli jest to przedmiot metalowy, stosuje się prawo mówiące o rozszerzaniu się metalu pod wpływem wysokiej temperatury. W wyrażeniu tym występują zmienne i symbole stałe wzbogacone w stosunku do symboli występujących w rachunku zdań.

Symbol lub EL,. jest to symbol kwantyfikatora dużego lub ogólnego, niekiedy nazywanego również kwantyfikatorem generalnym. Tak rozumianemu kwantyfikatorawi odpowiadają w języku naturalnym wyrażenia typu każdy, wszelki, dowolny, dla każdego, dla dowolnego.

Symbol T reprezentuje predykaty (własności lub stosunki), które przysługują przedmiotom rozważanego zbioru — nazywamy je symbolami predykato-wymi. Predykaty mogą być wieloargumentowe.

Symbol x, y, z reprezentuje przedmioty (indywidua) danego rodzaju, które nazywane są symbolami zmiennych indywidualnych.

Symbol V łub 2^ jest symbolem kwantyfikatora małego, nazywanego niekiedy kwantyfikatorem szczegółowym, a także kwantyfikatorem egzystencjalnym. Czytamy: dla pewnego x istnieje takie x, niektóre x. Oto kilka przykładów formuł zdaniowych z użyciem symboli rachunku kwantyfikatorów.

A_x P_(i) (dla każdego x P od a-) Jest to schemat zdania np. wszyscy jesteśmy omylni.

~A_tP_(j) (nieprawda, że dla każdego x P od x). Jest to schemat zdania np. nie każdy jest bezinteresowny.

Użycie kwantyfikatora pozwala podkreślić powszechność określonej właściwości w stosunku do określonego zbioru przedmiotów czy indywiduów. Inaczej mówiąc, pozwala na osiąganie właściwego stopnia ogólności danego stwierdzenia. Stąd używając w logice rachunku zdań symboli kwantyfikatorów i wiążąc je z określoną formułą zdaniową, podkreślamy bądź jej charakter ogólny czyli, że odnosi się ona do zbioru wszelkich zdań, które będą zbudowane w taki sam sposób, bądź podkreśla się, że dziedzina zdań prawdziwych zbudowanych na danej formule ma zasięg ograniczony.

Zagadnienia rachunku kwantyfikatorów, jak sądzę, są słuchaczom znane z racji studiowania niektórych działów matematyki wykładanej na naszej uczelni.

7.1.    TAUTOLOGIE RACHUNKU ZDAŃ

7.1.1.    Metoda zero—jedynkowa. Poprawnie zbudowane formuły rachunku zdań,-które przy wszelkich podstawieniach wartości za zmienne zdaniowe stają się zdaniami prawdziwymi, nazywamy tautologiami, czyli prawami logicznymi (o czym już mówiliśmy). Czy jakieś wyrażenie jest tautologią, czy nie, można sprawdzić podstawiając odpowiednie wartości na miejsce zmiennych i porównując efekt z tablicami odpowiednich funkcji. Należy przy tym sprawdzić wszystkie możliwości, których liczba odpowiada wzorowi 2", gdzie n oznacza liczbę zmiennych w formule. I tak w wyrażeniu p —* q mamy do czynienie z 2^Z = 4 możliwości, p —(q —> r) mamy 3 zmienne, czyli liczba możliwości wynosi 2ⁿ = 8.

W związku z problemem tautologii B. Stanosz czyni interesującą uwagę: „Celem formalno—logicznego opisu języka jest wyznaczanie zbioru zdań logicznie prawdziwych. Cel ten osiąga się poprzez 1° przyporządkowanie zdaniom ich form logicznych 2° ustalenie, które z tych form są tautologiczne, czyli formami zdań logicznie prawdziwych”⁵. Pierwsze zdanie wiąże się z gramatyką i tu jest niewielki udział logiki, głównie w postaci symboliki, drugie zaś jest całkowicie związane z logiką. Właśnie rachunek zdań wymaga zbioru takich form logicznych.

„Mówiąc, że dane zdanie jest prawdziwe na mocy znaczenia występujących w nim spójników prawdziwościowych i sposobu, w jaki zostało zbudowane za pomocą spójników ze zdań prostych, chcemy powiedzieć, że prawdziwe jest każde zdanie zbudowane tak samo za pomocą tych spójników z dowolnych innych zdań; innymi słowy — że prawdziwe jest po prostu każde zdanie, reprezentowane przez schemat prawdziwościowy, pod który podpada zdame dane. Takie schematy nazywać będziemy tautologiami rachunku zdań”.

Formuła rachunku zdań (logika zdań) jest tautologią tego działu logiki zawsze i tylko wtedy, gdy jest schematem wyłącznie prawdziwych zdań.

7.1.2. Wróćmy do przykładów weryfikacji tautologii metodą 0, 1. Zweryfikujemy metodą 0,1 np. zasadę wyłączonego środka: pv rap.

I. Za p podstawiamy 1    . II. Za p podstawiamy 0

1 v -1    0 v ~ 0

1 v 0    0 v 1

1 1 Zapis ten prowadzi zawsze do symbolu 1. Formuła ta jest więc tautologią.

A oto przykład: zasada sprzeczności ~(pA~p)

p/1 ~(1a~1)    p/O-COa-O)

-(1 a0)    -(0 a 1)

~o    -(0)

1.1

W podobny sposób można sprawdzać formuły logiczne bardziej złożone.

7.1.3. Tautologii rachunku zdań jest bardzo wiele. Poniżej zebrane tautologie są najbardziej znane wraz z ich symboliką i specjalnymi nazwami, które ustalały się w ciągu rozwoju logiki.

‘d 1. p -~p    zasada tożsamości (jeżeli p to p)

2.	~{P A ~p)
3.	pv~p
4.	P -~~(~P)
5.	~(~P) —P
6.	~{P ~^P) ~*P
7.	(P — ~P) ~	- ~P
8.	~P-+(P —	<?)
9.	~(pvq) =	~P A

zasada sprzeczności (nieprawda, że p i nie p) zasada wyłącznego środka (p lub nie p)

(jeśli p to nieprawda, że nie p)

prawo podwójnego przeczenia (jeżeli nieprawda, że nie p, to p)

prawo Claviusa prawo redukcji do absurdu prawo Dunsa Szkota Tlprawo De Morgana ⁶

JŁprawo De Morgana

' 10. ~(p/\q) s ~p\/~ą 11. (~p - ~q) - (q -*p)

v 12. {p — q) ~ (~q — ~p)

13.    (p-+q)A{p — ~q)~*~p

14.    ą—ip—ą)

prawo transpozycji prostej

prawo transpozycji prostej

prawo redukcji do absurdu z dwiema zmiennymi

prawo symplifikacji

15.    p Aq = qAp

prawo przemienności

16.    P^ą = qvp

17.    {p = q) = (q = p)

''■! 18. l{p-'q)/>p]—q 'i 19. [(p — ą)A~q)]-~-p 1, 20. [(p vq)A ~p] — q ' 21. [{p/q)Ap] — ~q

(czytaj: jeśli bądźp, bądź q i p,

22.    ~(p~>q)-(p- ~q)

23.    [(p->q)A(q-*r)J -~{p~*r)

24.    (pA ę-r) — [p — (g — r)]

25.    [p — r)] -*{pAq) — r

26.    (p — «)-*[(-p— q)-*q]

27.    (p —    — [(p — -9) — ~P1

modus ponendo ponens modus tollendo tollens ^ modus tollendo ponens u modus ponendo tollens to nie q)

prawo negacji implikacji prawo sylogizmu hipotetycznego prawo eksportacji prawo importacji prawo dylematu konstrukcyjnego prawo dylematu destrukcyjnego

Wiele praw rachunku zdań znano w starożytności, również średniowiecze ma swój wkład w teorię zdań. W postaci współczesnej rachunek zdań stworzyli G. Fręge, który ogłosił rachunek zdań w wersji impłikacyjno—negacyjnej oraz A. Whitehead i B. Russel z negacją i alternatywą.

7.1.4. Posłużymy się funkcją zdaniową bardziej złożoną, o której nie wiemy, czy jest prawdziwa, czy nie:

[(p^v9) —r]-*[p-*(9Ar)]

W celu wydzielenia całości syntaktycznych możemy posłużyć się techniką pomocniczą w postaci nawiasów.

			1	2	3	4
p	ą	r	pvq	(pvq)-y-	qAr	p-(qAr)	[(pvtf) —r] — [p — <?Ar)J
1	i	i	1	1	i	1	1
1	i	0	1	0	0	0	1
1	0	1	1	1	0	0	0
1	0	0	1	0	0	0	1
0	i	1	1	1	1	1	1
0	i	0	1	0	0	1	1
0	0	1	0	1	0	1	1
0	0	0	0	1	0	1	1

Za pomocą metody zero-jedynkowej wykazaliśmy, że badana funkcja zdaniowa nie jest tautologią rachunku zdań. Dokładna analiza tego przykładu pozwoli słuchaczowi zrozumieć samą operację weryfikacyjną.

Metodę zero-jedynkową można skrócić eliminując te sytuacje, kiedy mamy udowodnić końcową wartość 1.

Jeżeli udowodnimy, że kombinacja wartości, która powinna doprowadzić do wartości 0 (jak np. w implikacji p — q, jeżeli za p będzie 1, za q będzie 0), zawsze doprowadzi do wartości 1, tzn. że mamy do czynienia z tautologią.

7.1.5. Nie wnikając bliżej w sprawę, należy stwierdzić, że istnieją jeszcze inne metody dowodzenia tautologicznego charakteru funkcji. Jedną z takich metod jest aksjomatyzacja rachunku zdań, która polega na wymienianiu explicite twierdzeń, które postanawia się przyjąć bez dowodu.

Takie twierdzenia nazywamy aksjomatami lub twierdzeniami pierwotnymi, te natomiast, które się dowodzi na podstawie tych założeń, nazywają się twierdzeniami pochodnymi. Jest rzeczą oczywistą, że twierdzenia pochodne czy pierwotne ujawniają się dopiero w ujęciu całościowym systemu aksjomatycznego. Drugim elementem systemu aksjomatycznego są zasady dowodzenia zwane regułami inferencyjnymi.

Systemy aksjomatyczne logiki formalnej spełniają podstawowe wymogi: to znaczy każda prawda systemu musi być bądź aksjomatem, bądź twierdzeniem pochodnym. Spełniają one również wymóg, aby takie twierdzenia, tzn. aksjomaty i pochodne, były prawdziwymi twierdzeniami systemu. Udowodnienie prawdziwości tych stwierdzeń w odniesieniu do systemu aksjomatycznego rachunku zdań jest sprawą nieco skomplikowaną. Dlatego też tym zagadnieniem nie będziemy się zajmować. W trakcie wykładu będzie zademonstrowany jeden taki przykład.

7.1.6. Rachunek zdań można zbudować również metodą tzw. systemu założeniowego, w którym istotną rolę odgrywają odpowiednie reguły, np.:

—    odrywania,

—    dołączania koniuńkcji,

—    opuszczania koniunkcji,

—    dołączania alternatywy,

—    opuszczania alternatywy,

—    dołączania równoważności,

—    opuszczania równoważności.

7.2. ELEMENTY RACHUNKU NAZW

7.2.1.    Najprościej rachunek nazw lub teorię nazw, jak wolą niektórzy, można określić jako dział logiki formalnej obejmującej formuły, czyli wzory ze zmiennymi nazwowymi. Na miejsca zmiennych nazwowych można podstawić tzw. terminy, czyli nazwy ogólne i niepuste.

7.2.2.    Zdania, które są przedmiotem rachunku nazw, nazywają się zdaniami kategorycznymi,subsumpcyjnymi lubasertorycznymi.

7.2.3.    Język rachunku nazw. Symbolika rachunku nazw. Zmienne nazwowe oznaczane są dużymi literami alfabetu łacińskiego i jest ich trzy: S (łac. subiectum — podmiot), P (lac. praedicatum — orzecznik), M (łac. tenninus medius — termin średni). Symbole stałe funktorów zdaniotwórczych od argumentów nazwowyeh pochodzą od dwóch łacińskich słów — affiimo — twierdzę i nego — przeczę. Dwie pierwsze samogłoski z tych słów są symbolami funktorów, czyli a, i, e, o.

■ 12A. Podział zdań kategorycznych. Odpowiednie funktory klasyfikują zdania kategoryczne na poszczególne grupy, które zgodnie z charakterem funktorów należą do zdań twierdzących bądź przeczących — podział ze względu na jakość oraz ogólnych i szczegółowych — podział ze względu na ilość.

12.5. Krzyżując owe kategorie uzyskujemy następujący podział zdań kategorycznych na:

—    ogólnotwierdzące,

—    szczegóło wotw ie rdzące,

—    ogólnoprzeczące,

—    szczegółowoprzeczące.

Stosując odpowiednią symbolikę możemy poszczególne formuły zdaniowe przedstawić następująco:

1)    ogólnotwierdzące S a P czytamy: każde S jest P,

2)    szczegółowotwierdzące S i P czytamy: niektóre 5 są P,

3)    ogólnoprzeczące S e P czytamy: żadne S nie jest P,

4)    szczegółowoprzeczące S o P czytamy: niektóre S nie są P.

Zdania te można również zapisać używając prostej symboliki rachunku zbiorów i rachunku zdań.

I tak zdanie S a P może być zapisane:

A^ [(x e S) —* (x e P)], czytamy: dla każdego x jeśli x jest S, to x jest P.

Zdanie S e P:

A_x[(xzS) — (xzP)'], gdzie znak ' oznacza przeczenie, czytamy: dla każdego x,

jeśli x jest S, to nie prawda, że x jest P.

Zdanie S i P:

H_x [(x e S) a (x s P)] czytamy: istnieją takie x, że x jest S i x jest P.

Zdanie S o P:

[(x e S) a (x e P)'] czytamy: istnieje takie x, że x jest S i nieprawda, że x jest P.

Należy jeszcze zaznaczyć, że wszystkie funkcje zdaniowe sformułowane przez Arystotelesa, twórcę teorii zdań kategorycznych, zostały sformułowane z użyciem funktora implikacji jeślL.to i funktora koniugacji i.

7.2.6, Termin rozłożony. „Przez techniczne określenie »rozłożenie terminu« .rozumiemy użycie terminu w całym zakresie” . Praktycznie rozpoznajemy, czy termin jesfToźłóżonyrczy rńeTpó^tym czy stoi przed nim jawnie, czy domyślnie słowo każdy, ewentualnie żaden^{7 8}. Można tutaj przyjąć kilka reguł:

a)    W zdaniach ogólnotwierdzących rozłożony jest podmiot, a nierozłożony orzecznik, np.: każdy lekarz jest absolwentem Wyższej Szkoły Medycznej. Termin rozłożony — to lekarz.

b)    W zdaniach ogólnoprzeczących rozłożony jest zarówno podmiot, jak i orzecznik.

c)    W zdaniach szczegółowotwierdzących ani podmiot, ani orzecznik nie jest rozłożony, np. niektórzy ekonomiści są naukowcami.

d)    W zdaniach szczegółowoprzeczących nierozłożony jest podmiot, natomiast-

rozłożony jest orzecznik, np. niektóre kobiety nie są matkami, czyli: niektóre kobiety nie należą do klasy Ji&bżeT.    ;

Ogólna formuła na temat rozłożenia terminu brzmi:

TF zdaniach kategorycznych rozłożone są terminy figurujące w roli podmiotów zdań ogólnych oraz terminy będące w zdaniach przeczących orzecznikami.

7.2.7.    Prawa rachunku nazw odnoszące się do wnioskowania bezpośrednie-go. Między zdaniami kategorycznymi czyli subsumpcyjnymi, a ściślej między ich wartościami logicznymi mogą zachodzić różnorodne związki, które mają charakter wnioskowania. W rachunku nazw wyróżniamy dwa rodzaje wnioskowania i związane z tym prawa logiczne:

a)    wnioskowanie bezpośrednie, które polega na tymi, że do wniosku dochodzimy na podstawie jednej przesłanki;

b)    wnioskowanie pośrednie, kiedy wniosek wyprowadzony jest z dwóch przesłanek, przy czym odbywa się to z udziałem tzw. terminu średniego. Punkt wyjścia obydwóch wniosków nazywa się przesłanką, punkt zaś dojścia konkluzją.

7.2.8.    Podstawowymi zasadami wnioskowania bezpośredniego są konwersja, obwersja, kontrapozycja.

a)    Konwersja polega na wyprowadzaniu z klasycznego zdania kategorycznego jego odwrócenia i może występować w postaci prostej i z ograniczeniem.

Konwersja prosta polega na zmianie miejsca podmiotu i orzecznika. Konwersja z o g ran i c zeniem, oprócz zmiany jak w konwersji prostej, wprowadza jeszcze zmianę ilości zdania odwróconego.

I tak, konwersji prostej podlegają zdania ogólnoprzeczące i szczegółowotwierdzące. Zapis symboliczny tej zasady:

SeP —- PeS.

W tych przypadkach możemy użyć również symbolu tożsamości:

StP — PiS, SeP = PeS, SiP = PiS.

Na przykład: żaden koń nie jest psem = żaden pies nie jest koniem;

niektórzy ludzie są wegetarianami = niektórzy wegetarianie są ludźmi; niektórzy studenci są ludźmi wierzącymi zawsze i tylko wtedy, gdy niektórzy ludzie wierzący są studentami.

b)    Obwersja polega na wyprowadzeniu ze zdania twierdzącego równoważnego mu zdania przeczącego i na odwrót, ze zdania przeczącego wyprowadza się zdanie twierdzące.

Aby dokonać obwersji jakiegoś zdania kategorycznego, musimy zmienić przede wszystkim jakość a następnie dodać negację do orzecznika.

Zapis symboliczny: SaP — SeP' (czytamy: jeśli każde S jest P, to żadne S nie jest nie P).

Na przykład: jeżeli każda konstytucja jest ustawą, to żadna konstytucja nie jest nie-ustawą — to jest obwersja zdania ogólnotwierdzącego.

SiP — SoP' (czytamy: jeżeli niektóre S są P, to niektóre S nie są nie P); jeśli niektórzy ekonomiści fsT są biznesmenami, to niektórzy ekonomiści są nie-biz-nesmenami.

SeP —-■ SaP' (czytamy: jeżeli żadne S nie jest P, to każde S jest nie P)\ jeżeli żaden złodziej nie jest uczciwy, to każdy złodziej jest nieuczciwy.

SoP —* SiP' (czytamy: jeżeli niektóre S nie są P, to niektóre S są nie P).

Można we wszystkich wzorach obwersji postawić zamiast znaku implikacji znak równoważności, oznacza to możliwość wnioskowania w obydwie strony.

J. Gregorowicz pisze, że „Obwersja nie jest jakimś szczególnie płodnym rodzajem wnioskowania. Może jednak oddać pewne usługi przy rozstrzyganiu np. kwestii czy dwaj przeciwnicy, wypowiadający swoją tezę różnymi słowami, twierdzą to samo, czy też nie”.⁹

c) Kontrapozycja powstaje przez przestawienie i zanegowanie obu terminów zdania kategorycznego. Może występować w postaci prostej i ograniczonej.

Zapis symboliczny zasady kontrapozycj i^ p r o s t e j:

SaP —•P'aS' (czytamy: każde S jest P, to każde nie P jest nie S),

SoP — P'oS' (czytamy: jeśli niektóre S nie są P, to niektóre nie P nie są nie

S).    '

Prawa te mogą być zapisane z ujęciem równoważności.

Zapis symboliczny zasady kontrapozycii ogran iczonej:

SeP — P'oS' (czytamy: jeżeli żadne S nie jest P, to niektóre nie P nie są nie S).

7.2.9. Szczególnym przypadkiem związków między zdaniami kategorycznymi jest kwadrat logiczny, czyli opozycja zdań.

Obraz graficzny kwadratu logicznego: _f

SaP    Przeciwieństwo .SeP '

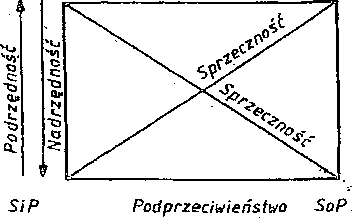
7.2.10. Z przedstawionych tu symbolicznie zależności wynikają bardzo ściśle zasady wnioskowania.

a)    Stosunek przeciwieństwa określają symbolicznie formuły:

SaP — (SeP)', czyli zachodzi tu stosunek równoważności SeP — (SaP)'.

Niepoprawne są wzory:

(SaP)'-SeP; (SaP)'.-{SeP)'; (SePj-SaP oraz (SeP)’ - (SaP)’.

b) . Stosunek, podprzeciwieóstwa zaś określają takie symboliczne formuły wnioskowania:

(SiP)’ — SoP,czytamy: jeśli nie jest tak, że niektóre S są P, to niektóre S nie są

\ ( (SoP)' — Sr Poczytamy: jeżeli nieprawdą jest, że niektóre S nie są P, to nie-które~S.sąP.

Nieprawidłowe"^ wzory:

SiP —SoP; SiP —(SoP)'; SoP —SiP, SoP —(SiP)'.

c) Stosunek sprzeczności zachodzi wtedy, kiedy zdania sprzeczne nie mogą-być ani zarazem prawdziwe, ani zarazem fałszywe.

Poprawnych jest osiem wzorów:

SaP - (SoP)’ (SaP)' —SoP SoP-(SaPy (SoP)' — SaP

SeP — (SiP)’ (SeP)'—SiP SiP — (SeP)' (SiP)' - SeP

d)    Stosunek nadrzędności. Jeśli zdanie nadrzędne jest prawdziwe, to zdanie podrzędne jest prawdziwe, natomiast jeśli zdanie nadrzędne jest fałszywe, to zdanie podrzędne jest nieokreślone.

Poprawne są dwie zależności:    _N

SaP —SiP,

SeP —SoP.

i

e)    Stosunek podrzędności jest odwrotnością stosunku nadrzędności. Jeżeli zdanie podrzędne jest prawdziwe, to zdanie nadrzędne jest nieokreślone, a jeśli zdanie podrzędne jest fałszywe, to nadrzędne jest fałszywe. Występują więc dwa wzory:

(SiP)'-(SaPy,

(SoPy—(sipy.

S. WNIOSKOWANIE POŚREDNIE. SYLOGIZM KATEGORYCZNY

8.1. Wnioskowanie sylogistyczne określa się jako wnioskowanie z dwóch lub więcej przesłanek. Uważny słuchacz zetknął się już z tym problemem w teorii zdań. Określa się go również mianem wnioskowania pośredniego właśnie z tego-powodu, że między przesłanką a wnioskiem znajduje się jeszcze jedna przesłanka pośrednia. Na przykład [(p —'> q) A(q — r)] —• (p —r). Można bez trudu zauważyć, że wnioskowanie sylogistyczne posiada zawsze więcej niż dwie zmienne.

8.2. .SYlogizm kategoryczny, jak nie trudno się domyśleć, skonstruowany jest ze zdań kategorycznych.

Oto przykład konstmkcji zdaniowej:

każda zbrodnia jest przestępstwem; każdy rabunek jest zbrodnią, _

A więc: każdy rabunek jest przestępstwem.

Można to zdanie zapisać za pomocą znanej już symboliki rachunku nazw: / W    '

,) MaP w postaci implikacji

SaM ^    (MaP a SaM) —■ Sap

i

SaP

K

Każde‘'zdanie "poprzednika tej implikacji nazywa się przesłanką, czyli przesłanką jest M a P i S a M, następnik zaś jest wnioskiem, który w tym przypadku nazywa się konkluzją. Ta przesłanka, która zawiera orzecznik konkluzji, nazywa się przesłanką większą, ta zaś, która zawiera podmiot konkluzji jest prze-sianka mniejszą.

Nazwa taka wynika jeszcze ponadto z faktu, iż zakres nazwy będącej orzecznikiem konkluzji jest szerszy od dwóch pozostałych zakresów nazw. Stąd też termin (nazwa) będący orzecznikiem konkluzji, czyli w cytowanym przykładzie termin oznaczony symbolem P nazywamy terminem większym a oznaczony symbolem S — terminem mniejszym.

Natomiast termin, który powtarza się w obydwóch przesłankach, nazywamy terminem średnim. W trybie sylogistycznym umownie przyjęto najpierw umieszczać przesłankę większą. Warto podkreślić, że w sylogizmie hipotetycznym elementem wspólnym jest zdanie a w sylogizmie kategorycznym nazwa.

8.3. Formy sylogizmu kategorycznego mogą być różne i dzielą się na cztery typy zwane figurami, różniące się od siebie miejscem terminu średniego.

	Figura I	Hgura II	Figura III	Figura IV
	MP	PM	MP	PM
	SM	SM	MS	MS
	SP	SP	SP	SP

Aby mogło nastąpić wnioskowanie, poszczególne figury muszą być wypełnione odpowiednimi funktorami, które zamieniają układ symboli w schematy zdań różniących się ilością i jakością, czyli w zdania bądź to ogólnotwierdzące, ogólnoprze-czące, szczegółowotwierdzące, szczegółowoprzeczące. Taki zabieg można wykonać wstawiając do figur znane już litery a, e, i, o.

8.4. Tak powstałe schematy wnioskowania nazywają się t r y b a m i. Na przykład:

M a P    jest trybem figury I zbudowanym przez wstawienie funktorów,

S a M    symbolizujących zdanie ogólnotwierdzące, między symbole

y _a p ’ zmiennych nazwowych.

Oto przykłady innych trybów zbudowanych na bazie figury I, z użyciem innych funktorów:

M eP-	MaP	MeP
SaM	SiM	SiM
Se P	Si P	SoP

8.5. Wszystkich możliwych trybów, a więc schematów wnioskowania opartych na czterech figurach, jest 256, z tym, że poprawnych jest tylko 24. Ażeby ułatwić zapamiętanie trybów poprawnych w średniowieczu wymyślono odpowiednie pomocnicze wyrażenia o charakterze mnemotechnicznym, to znaczy pomagają one zapamiętać odpowiednią kolejność funktorów, ale same nie posiadają żadnego znaczenia. Przyporządkowane są odpowiednim figurom po 6 do każdej. Służą pomocą w ten sposób, że zawarte w nich symbole funktorów wstawia się kolejno do przesłanki I, II i konkluzji.

Przytaczam zapis tych wyrażeń:

do figury I — BSibara"}Celarent, Darii, Ferio, Barbari, Celaront; do figury II — Cesare, Ćamestres, Festino, Baroco, Cesaro, Cąmestros; do figury HI — Darapti, Dismais, Datisi, Felapton, Bocardo, Fąrison; £ do figury IV — Bamałip, Całemes, Dimatis, Fesapo, Fresison, Calemos.

8.6.    Pośród sylogizmów można wyróżnić tryby doskonałe, których nie trzeba dowodzić i które pełnią rolę aksjomatów, służąc tym samym do udowadniania pozostałych sylogizmów. Takie sprawdzanie nazywa się niekiedy redukcją trybów niedoskonałych do doskonałych. Do trybów doskonałych zaliczamy: Barbara, Celarent.

8.7.    Oprócz metody alcsjomatycznej weryfikacji poprawności trybów można jeszcze stosować dwie inne; jedna to tzw. warunki niepoprawności, a druga diagramy Venna.

8.8.    Niepoprawny jest sylogizm, który' posiada:

a) Więcej niż trzy terminy. Zdarza się to w szczególności, gdy termin szeroki użyty jest w dwóch znaczeniach¹⁰.

Każdy zamek jest okazałą budowlą	Mj a P
Każdy suwak jest zamkiem	S a M2
Każdy suwak jest okazałą budowlą	SaP

b) Termin śrpdkowy ani razu ni ero złóż

Każdy ptak jest stworzeniem dwunożnym	PaM
Każdy człowiek jest stworzeniem dwunożnym	SaM
Każdy człowiek jest ptakiem	SaP

i

ony.

c) O b i e przesłanki przeczące.

Żadna kobieta nie jest mężczyzną	MeP
Żadna kobieta nie jest ojcem	MeS
Żaden ojciec nie jest mężczyzną	SeP

Niektóre zwierzęta są kotami	M i P
Niektóre zwierzęta są psami	M i S
Niektóre psy są kotami	S i P

e) Termin większy lub mniejszy rozłożony w konkluzji a nierozłożony w przesłankach.

Każde prawo jest związane z interesem społecznym	M a P
Żadne społeczeństwo nie jest prawem	SeM
Żadne społeczeństwo nie jest związane interesem społecznym	S e P

f) Konkluzję twierdzącą, gdy jedna przesłanka jest przecząca.

Każda zbrodnia jest karalna	M aP
bl^które czyny ludzkie^zB^odniami	So M
K^ly czyn ludzki jest karalny	SaP

g) Konkluzję ogólną, gdy jedna z przesłanek jest szczegółowa.

Każdy adwokat jest prawnikiem	MaP
Niektórzy ludzie są adwokatami	S i M
Każdy człowiek jest prawnikiem	SaP

h) Konkluzję przeczącą, gdy ani jedna z przesłanek nie jest przecząca.

Każdy uczciwy człowiek jest zwolennikiem pokoju	MaP
Niektórzy obywatele Polski są ludźmi uczciwymi	S i M
Żaden obywatel Polski nie jest zwolennikiem pokoju	S e P

1

   Mała encyklopedia logiki. Ossolineum, Wrocław-Kraków-Warszawa 1988.

2

   T. Kotarbiński: Wykłady z dziejów logiki. PWN, Warszawa 1985.

3

2. Ziembiński: Logika praktyczna. WN PWN, Warszawa 1994, s. 89.

4

Ibid., .s. 23.

5

B. Stanosz: Wprowadzenie do op. cit, s. 29.

6

Ibid., s. 29.

7

* J- Gregorowicz: Zarys logiki dla prawników. PWN, Warszawa 1962, s. 107.

8

Ibid. .

9

Ibid., s. 113.

10

Wszystkie przykłady tu podane pochodzą z pracy J. Gregorowicza: Zarys logiki dla prawników. PWN, Warszawa 1962.