majza3

1. Dwie kule: białą i czerwoną wrzucono „na chybił trafił" do pięciu szuflad oznaczonych cyframi 1, 2, 3, -1 i 5. Wyznacz przestrzeń zdarzeń elementarnych oraz zdarzenia: A - w szufladzie nr 5 nie ma kuli czerwonej, B - w szufladzie 4 jest co najwyżej I kulo. Oblicz prawdopodobieństwa: P(A). P(B), P(ĄoB), P(AoB). Sprawdź niezależność zdarzeń A i B

2 Na sali jest 12 ławek w 3 rzędach. Pięciu studentów losuje miejsca na sali. Jakie jest prawdopodobieństwo, ze studenci B i C będę siedzieli jeden za drugim?

3. Egzamin z matematyki odbywa się w trzech salach: 169. 180 i 265. Prawdopodobieństwo zdania egzaminu w sali 169 wynosi 70%. w sali 180 wynosi 40%. a w sali 265 30%. Student wybiera salę rzucając kostkę: jeśli wyrzucona liczba oczek jest podzielna przez 3 wchodzi do sali265, jeżeli wypadnie 5 wchodzi do sali 180, w pozostałych przypadkach idzie do sali 169. Obliczyć:

a)    prawdopodobieństwo tego, ze student nic zda egzaminu;

b)    prawdopodobieństwo warunkowo tego, ze wybrany student zdawał egzamin w s. 169, jeżeli wiadomo, ze go zdał.

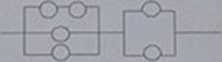
A. Oblicz niezawodność układu, przy założeniu, że przekaźniki działają niezależnie i niezawodność każdego z n:ch wynosi q=0.7S

5.    Prawdopodobieństwo trafienia na wartościowego pracownika, o odpowiednich predyspozycjach na dane stanowisko, wynosi 0.3. Jakie jest prawdopodobieństwo. że na 7 kandydatów, jest co najmniej 3 o odpowiednich predyspozycjach?

6.    Uczestnik zawodów strzeleckich trafi3 do celu z prawdopodobieństwem 0,8. Po pierwszym trafieniu przerywa strzelanie Maksymalna liczba strzałów, które może oddać wynosi 5. Niech X oznacza liczbę zużytych naboi przez uczestnika zawodów strzeleckich. Oblicz wartość oczekiwaną zmiennej X, oraz o.