P1040849

Plaski stan naprężenia w punkcie może być przedstawiony graficznie za pomocą kola Mohra. Kołem Mohra nazywamy miejsce geometryczne punktów płaszczyzny (o, t) charakteryzujące się tym, że współrzędne tych punktów sil odpowiednio naprężeniem normalnym i stycznym dla tego samego stanu naprężenia w punkcie przy różnych kątach obrotu układu współrzędnych. Równanie koła (ściśle - okręgu) Mohru ma postać

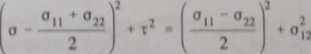
*!■ n

Rys. 1-2. Transformacja układu współrzędnych w stanic płaskim

Punkty przecięcia osi o przez koło Mohra (rys. 1.3) wyznaczają naprężenia główne Oj i o₂. Kąt między promieniem OP i osią o jest podwojonym kątem a . Należy zwrócić uwagę, że dodatnie kąty <p i a₍ odmierzane są na rysunku przedstawiającym koło Mohra przeciwnie niż na rysunku pokazującym obrót układu współrzędnych.

Stan odkształcenia w punkcie, podobnie jak stan naprężenia, jest tensorem, ten. obiektem opisanym przez 9 liczb: t_M, y , y_a. Y„. *,• Y*. Y„. Y*. V zależnych od orientacji układu współrzędnych. Elementy diagonalne macierzy stanu odkształcenia są wydłużeniami względnymi w kierunkach osi współrzędnych, pozostałe elementy są kątami odkształcenia postaciowego. Deformacja kwadratu ABCD, pokazana na rys. 1.4 prowadzi do następujących składowych płaskiego stanu odkształcenia

X

A' B' costt - AB AB

y

A'D‘ cos a - AD AD

P

Liczby c_x, i ^ w pełni określają deformację kwadratu. Macierz stanu odkształcenia ma postać

T -

•u 'u

*21 *22

(1.7)

gdzie: «„

" *,• *22 * V *12 * *21 *

11