P1000271
.. j*+tn\,£.yc ekstrema lokalne funkcji f(x) m x2 lnx 2. Wyznaczyć ekstrema lokalne funkcji:
f(x,y,z) = x2 - y2 + z2 - 2xy + 2yz + 4y - 2z + 5
. Obliczyć pole obszaru ograniczonego krzywymi:
y - - x2 + 5x - 4
x + y + 4 = 0
L Obliczyć granicę ciągu : lim( 1 i I-r )5n+ 1 =
W">4-00 3Ti — 2
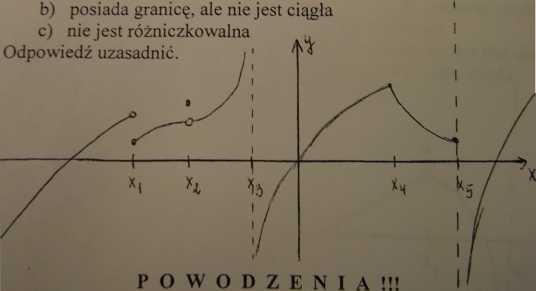
Wśród xj, X2, X3, X4, X5 wskazać punkty, w których funkcja f: a) nie posiada granicy
Wyszukiwarka
Podobne podstrony:
Mechanika kwantowa Stan układu złożonego z N cząstek określa funkcja falowa Y (x1( yuzu x2, y2, z2,.
płaszczyzna w przestrzeni PŁASZCZYZNA W PRZESTRZENI Oznaczenia: II- płaszczyzna P = (x,y,z) P* =(x0,
Równanie płaszczyzny przećliodzacej przez 3 pkt Pl(xl,yl,zl), P2(x2,y2, z2), P3{ x3.y3.z3).
Scan10002 SFERA S : x2 + y2 +z2 = R2 S = Si U S-2 Si: z= y/R2 —
płaszczyzna w przestrzeni PŁASZCZYZNA W PRZESTRZENI Oznaczenia: II- płaszczyzna P = (x,y,z) P* =(x0,
57 (245) 1) Obliczyć masę bryły V, ograniczonej powierzchniami: x2 + y2 + z2
68 3. Zbieżność ciągu - Zbiory domknięte 3.20. Niech będzie S = {(x,y,z) € R3 : x2 4- y2 -ł- z2 — l}
DSC01679 (6) ad.l. Oblicz masę bryły B: x2+y2+z2<9 leżącej w pierwszym oktancie układu współrzędn
algebra 4 01 10 cz4 SFERA 5 : x2 + y2 + z2 = R? S = S h U S -2 Si : z - y/R2 - x2 - y2; (x,y)
Scan10002 SFERA S : x2 + y2 +z2 = R2 S = Si U S-2 Si: z= y/R2 — x2 — y2 (x,y) € D
poprawa z rozniczek2 Zadanie 3. (5p) Wyznaczyć ekstrema funkcji /(x, y) — y In (y + 2x2). Si: z = 12
973688I4935260575205?2156197 n Zadanie 3 (3p) Wyznacz ekstrema lokalne funkcji f(:c, y) = :,;2 + xy
Fitopatologia 5 również po istnieniu **%Jb6cTy<*lub «•* do"*tn,e »!< ł« ro *!„_ środko
skanuj0010 (176) % 2S*>Q ^ j_______V" A ■ 0 ^ x £ *c *c/T- <y Yc£ y-ź
więcej podobnych podstron