Scan10051

^4-r² =t

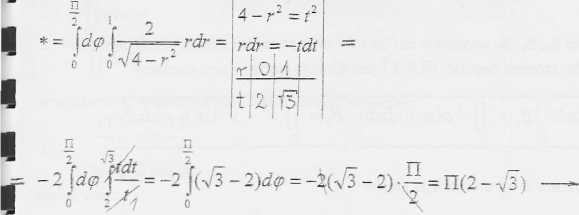
—f ^|= 80(2 - V3 )    ^

Zastosowania całki podwójnej w mechanice.

Masa

Masa domkniętego obszaru regularnego D, którego gęstość P(^x>}^!) to funkcja ciągłą w D, jest równa:

jM = j \p{x, y)dxdy\

j. d    i

W przypadku, gdy 3 obszar jest jednorodny tzrt. P\^x>y) — 1 to M — |^dxdy — \D\ d

Momenty statyczne

Momenty statyczne M_x I M_y względem osi GX i OY regularnego obszaru D, którego gęstość P\^x>y) jest funkcją ciągłą w tym obszarze, określają całki podwójne w postaci:

m = ffyp(x,y)cźxcty\\M_y = ffxp(x,y)dxdy\

I D    f l D    i

TWIERDZENIE

Współrzędne środka ciężkości Xo .i yo:S(x₀,yo) regularnego obszaru D, którego gęstość jest fUnkcją ciągłą W tym obszarze, określają wzory:

Mjl

M

mm

Mi

M