stany nieustalone str18

i{t) = C ^^U(    sin(<2tf + y/ - ę?)

^w dt Z ^v    7

1

cos(^-^> ^r ₍₁26)

Stalą czasowa, tak jak przy wymuszeniu stałym, wynosi x = RC.

Do wyznaczenia przebiegów czasowych napięcia na kondensatorze i prądu ładowania kondensatora zastosowaliśmy wprawdzie metodę operatorową, ale podobnie jak w metodzie klasycznej zastosowanej do analizy stanu nieustalonego w gałęzi szeregowej R,L, odpowiedź jest wyrażona w postaci dwóch składowych: składowej wymuszonej i składowej swobodnej (przejściowej).

Składowa przejściowa w miarę t->oo maleje wykładniczo do zera.

W zależności od fazy początkowej \\i napięcia wymuszenia oraz od kąta cp możemy podobnie jak dla gałęzi szeregowej R, L wyróżnić dw a przypadki graniczne

.X

(a)    V~<P=±

<b)^-(Z> = 0

W przypadku granicznym (a) w chwili komutacji składowa ustalona napięcia na kondensatorze przechodzi przez zero, składowa przejściowa jest równa zeru, a więc osiągamy od razu stan ustalony w obwodzie.

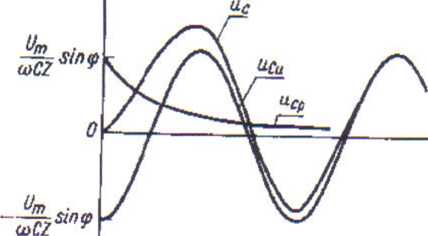
Rys. 13.Przebiegi czasowe napięcia na kondensatorze w gałęzi szeregowej R, C przy wymuszeniu sinusoidalnie zmiennym i fazie początkowej i//=IJ/2

W przypadku granicznym (b) w chwili komutacji składowa ustalona napięcia na kondensatorze przechodzi przez ekstremum.

Wtedy składowa przejściowa napięcia na kondensatorze ma w chwili początkowej największą z możliwych wartości i napięcie na kondensatorze w stanie nieustalonym osiąga wartość bliską podwójnej amplitudy wynoszącej U_n,/coCZ.

Na rysunku 13 przedstawiono wykres zmienności w funkcji czasu napięcia na kondensatorze dla

2007-01-10

18

TO/ES