P1010922 (5)
\dt I dt
^———2sm 22 cos 2tj dt
dt
2 sin 2f)2 +• (2cos 2źf

czyli p = —=6
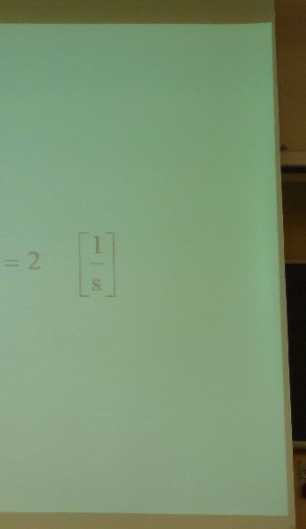
Wyszukiwarka
Podobne podstrony:
53729 P1010922 (4) dt 1 V = —v —> p = dt • P dt dt
Image1827 x = 2arctgf, dx = 2 dt 2 sin sinx =- • 2 x sin — 2 x cos — 2 cos cosx = 2 2 X cos — 2
Przykłady 1. r dx sin x R(n,v) = ł Ir = cos x R(- u,v) = -/?(//, vdt = - sin xdx r — s
Transformacja Laplace a w4 Wzór 4: / (?) = sin cot AR.es > O OD 03 F (j) = L {/
MAT18 18 2(1 l / -> 1 7 _et_= r_z±T_= r +1 )dt = sin.v(
MechanikaA4 a X = a r1.2 1Qmm —t + v. dt +v0t+C2 Z warunku początkowego: x(0) = 0, czyli CM 2 1 4)m
57 (256) wzoru: Pp + Y ap (23.22) Oznaczenia i tablicę pomiarową podano w poprzednim punkcie ćwiczen
P1010918 (4) iadanie: iuch punktu marerialnego określony jest równaniem
P1010918 (4) iadanie: iuch punktu marerialnego określony jest równaniem
40787 P1010920 (4) wektor przyspieszenia normalnego i jego wartość:UH = a,,ń Jeżeli a, =0 to £tn =a
więcej podobnych podstron