ts kolos2

21A TS KOLOKWIUM KOŃCOWE GRUPA: B

27-01-2012

2IA

Iml# i nuwMto (KfM|M Mmmmi)

łhwńlt pryjsiif » wyfeśue l mawnn* pUmo Podteai ubllcttń naUiy Młotować odnośna komtrnUtne (lub rytunkś) wtaoy fttti r6w»ud hdt p*MtyMwimlu, ti Ute O^ttn tom wynik

tSmhMjm Zmi t - Spkt„ Skuł 2 - JOpki, lad 3 - 20pkt„ Zad 4 - lOpkl., Zad, 3 - lipki

W przestrzeni £^J(-2,2) narysować, możliwie Jak najdokładniej, sygnał .»(/) fi( sini 2e7) i. #«W Obi ICJtyti składową stałą (ego sygnału. Odpowie di naloty uzasadnić I

V 2. obliczyć (doprowadząjąc do iak najprzejrzystszej postaci) widmo Fouriera    »ygnębi

,«•(/) • .1 4 sin 100*7 -

3*

4

Narysować (możliwie jak najdokładniej) charakterystykę c/ęemfliwpSełową

(amplitudową i fkzową). OdpowiedŁ uzasadnić.

3, Oblicayd (doprowadząjąc do jak ni\|przejrzystszej postaci) widmo Fouriera sygnału »(/)*2 lUr/2't) Narysować charakterystykę amplitudową i fazową. Zakładając, że sygnał byłby /definiowany w /,*(0,4)

a.    zaznaczyć na wykresach związek widma Fouriera z szeregiem Fouriera (możliwie jak najdokładniej),

b.    podać wzór analityczny opisąjący l harmoniczną sygnału s(/).

c.    narysować w dziedzinie czasu sygnał jr(f) wraz z pierwszą harmoniczną (możliwie jak najdokładniej).

4. Dla sygnału s(ł) • sin(2*t) w przestrzeni I^a(0,l):

a. obliczyć ciągłe widmo Talkowe (zgodnie z założeniami Daubechies), korzystając np. z lalek H*ar*s,

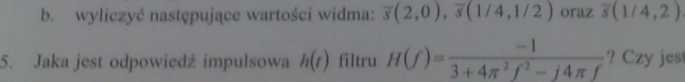
łtufoty uzasadnić/

? Czy jest to filtr subiln/' OdpowUdi