010 bmp

Odchylenie średnie kwadratowe średniej arytmetycznej serii

{n — \)n

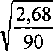
0,17 [V],

S, =

Zaokrąglając uzyskane wartości w górę do jednego miejsca znaczącego zgodnie z ogólną zasadą zaokrąglania wyników końcowych [2], otrzymamy U = 8 [V], s_r = 0,2 [V]. Niepewność średniej arytmetycznej serii wyrażona za pomocą błędu granicznego wynosi ±0,6 [V] z prawdopodobieństwem 98,5% ([4] - tablica dystrybuanty rozkładu Studenta). Wynik poprawiony serii pomiarów

£/=8 ±0,6 [V].

Wartość średniego odchylenia kwadratowego jednego pomiaru w danej serii wynosi

.v = j^ = °,55 [v]=0,fi [v].

Natomiast niepewność pojedynczego pomiaru wartości napięcia uwzględniająca błędy graniczne e: = 1,8 [V], e₂ = -1,8 [V] wynosi ±1,8 [V]. Wynika stąd, że z podanym prawdopodobieństwem uzyskane w serii wyniki pomiarów o wartości U > 9,8 [V] lub U < 6,2 [V] są omyłkami, których nie należy uwzględniać przy opracowywaniu wyników.

Przykład 2

W układzie jak na rysunku 1.2 wyznaczono pośrednio rezystancję R opornika, mierząc sześciokrotnie napięcie oraz prąd woltomierzem i amperomierzem. Dzięki zastosowaniu mierników o dużej dokładności (klasa laboratoryjna) i dobraniu amperomierza o rezystancji wewnętrznej znacznie niniejszej od przypuszczalnej wartości mierzonej rezystancji błędy systematyczne zostały pominięte jako małe w stosunku do błędów przypadkowych.

Wyniki pomiarów napięcia U i prądu / ujęto w tabeli 1.1.

Tabela 1.1

I	1	2	3	4	5	6
C/i [V]	10,6	11	10,3	10,7	10,5	10,4
A [A]	21	21,9	20,7	21,5	21,2	20,9

Wartości średnie napięcia i prądu:

U =

LU,

i-l

^=10,58 [V] = 10,6 [V], 6

-    127 2

/ _{=    =} izJjz. = 21,2 [mA].

6 6

Wartość średnią rezystancji R wyznaczono z zależności (1.19) przy uwzględnieniu związku (1.29)

R = ^ = -^10,6 = 504,76 [Q] * 504,8 [Q].

I 0.0212

Wartość średniego odchylenia kwadratowego średniej arytmetycznej pomiarów napięcia

s_fL! i prądu s_r! wyznaczono z zależności (1.26):

5-6

0,31

30

= 0,1 [V],

Ż(W)²    fi96

£, -11^.    ^;    = 0,18 [mA] = 0,2 [mA].

5-6

30

Wartość średniego odchylenia kwadratowego średniej arytmetycznej pomiarów rezystancji

s_rR wyznaczono z równania (1.30):

dR_

dU

V

, .fatY , _ hY , i u

97

=

“ 1 ^SrU ⁺ T2    ’

(21,2 • 10“³)²

^=6,6 [a].

(o,d³ + _&ML_. (0,2 ■ io'³)²,

(21,2*10 )‘

Wynik poprawiony serii pomiarów wynosi

R ± 3s_rR = 504,8 [Q] ± 19,8 [Cl].

Podczas pomiarów przyrządami cyfrowymi oprócz omówionych wyżej błędów występujących w analogowej części toru pomiarowego należy uwzględnić błędy, które wynikają z dyskretnego charakteru sygnału pomiarowego występującego w cyfrowej części toru pomiarowego. Zagadnienie wyznaczania tych błędów przedstawiono w rozdziale 9.

21