010

Z\ = o + 6i = 0) nebo je d = 0 a c = 0 (także je z₂ = c + di = 0). V każdem pffpade je tedy aspoń jedno z ćisel z\, z₂ rovno nule a du-kaz je tim proveden.

Zaverem jeśte poznamenejrne, że na zakladć komutativnosti a asociat.ivnost.i sćitani a nasobeni komplexnich ćisel lze ukazat, że pro mocniny komplexnich ćisel s prirozenymi exponenty plati stejna pravidla jako pro mocniny ćisel realnych:

Pro libovolna komplexni ćisla z, Z\, z₂ a v§echna pfirozena ćisla. n, m plati:

z^m • zⁿ = z^m+n, (_Zlz₂)ⁿ = ĄĄ,    (z^m)ⁿ = z^mn

Pro mocniny imaginarni jednotky dostanete snadno, że plati i² = -1,    i³=i²-i = -i, i⁴ = i² - i² = 1,

a obecne pro libovolne pfirozene ćislo k

i^4fc+1=i, i^4fc+2 = -l, i^4fc+3 = -i, i^4fc=l.

Shrneme-li dosavadni vysledky, mużeme konstatovat, że v obo-ru komplexnich ćisel mużeme bez omezeni sćitat, odćitat a nasobit. Dćlenim komplexnich ćisel se budeme zabyvat v nasledujicim ćlanku.

Priklad 2

Pfesvedćte se o spravnosti nasledujiciho vypoćtu:

(1 - i)(3 + 2i)² - 2(—3 - 2i) = (1 - i)(5 + 12i) - 2(-3 - 21) = = 5 + 12i — oi + 12 + 6 + 4i = 23+ lii

Ulohy

1.11    Dokażte, że sćitani i nasobeni komplexnich ćisel je komutativni a asociativni.

1.12    Urćete, pro ktcra komplexni ćisla je jejich soućet, resp. soućin ćislo

a) realne,    b) imaginarni, c) ryzę imaginarni.

c) i + i² + i³ + i⁴ + ... + i⁵⁰ d) 1 + i⁴ 4- i⁸ + i¹² -t- ... + i⁵²

1.13 Vypoćtete:

a) i³ + i¹³ + i²³ + i³³ + i⁴³ b) i • i

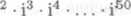
1.14    Vypoćtete:

a)    [(1 + 2i) — (3 — i)](l — i)²

b)    [(1 + 2i) — (3 — i)]²(1 — i)

c)    3(—1 + i)(l — i) — i(2 — 3i)

d)    (v/2 — iN/5)    -ł- (v/3 — i\/2) iv^2

1.15    Urćete realna ćisla a, b tak, aby platilo:

a)    (1 - i)o - (-2 + i)6 = 5 - 2i

b)    (V^ + i\/2)a-(v^/2 + iv/3)f>-l = i²-i

1.4 Deleni komplexmch ćisel, komplexm ćisla sdruzena

Komplexni ćisla uż iimime sćitat, odćitat, nasobit a umocfiovat. prirozenym oxponentem; nyni se budeme zabyvat. jejich delenim. Neź vśak k tomu pristoupime, zavedeme pojem komplexni ćislo sdruźene s danym ćislem.¹)

Komplexni ćislo sdruźene s ćislem a+ bi je ćislo a — bi.

Ćislo sdruźene s komplcxnim ćislem z znaćime obvykle ź (z s pru-hem). Pro ilustraci: s ćisly z\ = 2 + 3i, z^ = 1 — i, 23 = |i, 24 = 25, 25 = 3 - \/2 jsou sdruźena ćisla ~z{ — 2 — 3i, 22 = 1 + i, 23 = —|i, 2^ = 25, 25 = 3 + y/2. PiSeme też: 2 + 3i = 2-3i, 1 —i = l + i,

3

2

-fi, 25 = 25, 3 - \/2 = 3 + \/2.

19

1

) V nekterych ućebnicich matematiky se nusto terminu kornplexni (islo sdruźene muzete setkat s terminem ćislo komplexnć sdruźene.