0037

38

I. Teoria granic

to otrzymujemy ciąg

13    13    13

’ 2 ’ 3 ’ 4 ’ 5 ’ 6 ’

Również w tym przypadku x„->0, ponieważ

i i ³

|x„|<—<s n

dla ri> 3je, tak że za N, można przyjąć [3/e].

Spotykamy tu pewną osobliwość; wyrazy ciągu na przemian to zbliżają się do swej granicy 0, to oddalają się.

3) Niech teraz

1 +(-1)"

—    I

ciąg ten występował już w końcu ustępu 22. Tutaj także x„->0, bo

i ,    ²

*■<—<«> n

jeżeli tylko n>JV,= [2/e].

Zauważmy, że dla wszystkich nieparzystych wskaźników n wyrazy ciągu są równe swojej granicy. Te proste przykłady są interesujące dlatego, że charakteryzują rozmaitość tych możliwości, które objęte są danym powyżej określeniem granicy ciągu. Nie jest istotne, czy wyrazy ciągu leżą po jednej stronie granicy, czy nie; nie jest istotne, czy różnica wyrazu ciągu i granicy z każdym wzrostem wskaźnika jest coraz mniejsza; nie jest istotne wreszcie, czy ciąg osiąga swą granicę, tj. czy przyjmuje wartości równe granicy. Istotne jest tylko to, o czym mówiliśmy w definicji: wyraz ciągu powinien różnić się od granicy dowolnie mało, poczynając od pewnego wskaźnika, tj. dla dostatecznie dalekich wskaźników.

4) Rozważmy bardziej złożony przykład ciągu:

n² — n + 2 3n² +2n—4 ’

udowodnimy, że granicą ciągu jest liczba j. W tym celu rozważmy różnicę

-5n + 10 3 (3n² +2/i—4)

i oceńmy jej wartość bezwzględną; dla ri>2 mamy:

₁₍_    5n-10    ___    5/i    5/i    1

^"^_*'~3(3/i² + 2/i-4)^<3(3/i²— 4)^<3 • 2/i^{2 <}TT’

czyli wyrażenie jest mniejsze niż e, jeżeli n>N_Ł= [1/e]. Udowodniliśmy, że x„-/j.

5) Zdefiniujmy ciąg wzorem

x„=a^1/"= {/a    (a> 1);

pokażemy, że x„->l.

Korzystając z nierówności (3) z ustępu 19, możemy napisać, że

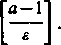
jx„—1|=V<»— i <- <fi, jeżeli tylko n>N_c—

n

Można jednakże rozumować inaczej. Nierówność

|x„ —l|=a^1/" —1 <e