0040

1

Tutaj

1-2

1

7

a₂--

§ 1. Ciąg i jego granica

i

¹ _ ^{1 1}

n(n +1) n n + 1 ’

41

czyli w tym przypadku

A„ =

2-3

1 1

2~ 3

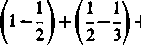
-LUi~L.

n + \j n + 1

Oczywiście    czyli szereg ten jest zbieżny i ma sumę 1.

Jeżeli szereg nie ma skończonej sumy, to mówimy o nim, że jest rozbieżny: takim jest np. szereg

26. Pewne twierdzenia o ciągu mającym granicę. Niech ciąg {x„} ma granicę a. Przy dowolnym p<a (lub q>a) łatwo dobrać liczbę £>0 tak, żeby było

a—e>p (lub a + e<q).

W tym celu wystarcza obrać e mniejsze niż różnica a—p (lub q—a). Ale, z definicji granicy [23] istnieje taki wskaźnik N, że dla n > N jest spełniona nierówność (por. (4))

x„ > a —e    (x„ < a + e),

a więc — tym bardziej — nierówność

x„>p (lub x_n<q).

1° Jeżeli ciąg {x„} dąży do a, oraz a>p (a<q), to również wszystkie wyrazy ciągu poczynając od pewnego są większe od p (mniejsze od q).

Z tego prostego twierdzenia wynika szereg użytecznych wniosków.

2° Jeżeli ciąg {*„} dąży do granicy a>0 (<0), to również sam wyraz x„>0 (<0), poczynając od pewnego miejsca.

Dla dowodu wystarcza zastosować poprzednie twierdzenie, biorąc p=0 (<7=0). Można otrzymać także wynik głębszy.

3° Jeżeli ciąg {x„} dąży do granicy a różnej od zera, to co najmniej dostatecznie dalekie wyrazy ciągu co do wartości bezwzględnej przewyższają pewną liczbę dodatnią r:

|x_n|>r>0 (dlan>N).

Rzeczywiście, przy a>0 (<0) można obrać

0 <p<a (a<q< 0)

i przyjąć r=p (r=\q\).

4° Z drugiej strony, jeżeli ciąg {*„} ma granicę a, to jest ograniczony w tym sensie, że wszystkie jego wyrazy co do wartości bezwzględnej nie przewyższają pewnej skończonej liczby:

|x„|<M (Af=const ; n = l, 2, 3,    .