0040

42

VIII. Funkcja pierwotna (całka nieoznaczona)

3) f ^d*---- f x-‘(l+x^s)-^,/3dx.

xy^l+x’

1    tn 4* 1

Tu m = —1, n = 5, p — —z-; drugi przypadek: - = 0, v = 3. Podstawmy

3    n

t = y'l—x⁵ , x = (t³ —    dx = -j t²(t³ — l)~^4lsdt;

mamy

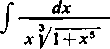
i f ^tdt

5 J /³-l

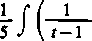
_£zJ_)_{A =} i.,_nj£nl)L

f²+r+l/    10 r² + f + l

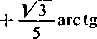
2/H-l

}/T

+ c

itd.

280. Wzory redukcyjne. Ponieważ całkę różniczki dwumiennej można przekształcić zawsze [patrz (2)] do postaci

J_p,_q = J (a + bz)^pz⁹dz ,

więc w dalszym ciągu ograniczymy się do rozpatrywania tych właśnie całek.

Wyprowadzimy kilka wzorów redukcyjnych, za pomocą których całka (3) może być, ogólnie rzecz biorąc, wyrażona przez podobną całkę Jgdzie p' i q’ różnią się od p i q o dowolne liczby całkowite.

Całkując tożsamości

(a + bz)^p+lz⁹ = a (a + bz)^pz⁹ + b (a + bz)^pz^9+l ,

[(a + 6z)^p+1z^<1+1] = (p + 1) h (a + hz)^pz^<,+¹ +(q + l) (a + bzY^+lz^Q ,

znajdziemy

•Ip + 1,9 “    P,ą + bJp,q + l >

(a + bź)^p+1z^9+l = (p + 1) bJ_p,_g+1+(q + l) J_p+U Otrzymujemy stąd dwa pierwsze wzory

(1)

Jp.Q ~

(a + 6z)‘^,+1z⁸⁺¹ p + q + 2

“r /•    . 4 \

a (p + 1)

a (p + 1)

(p ¥= -1) >

(II)

_T    (a + bz)^p+1z⁹⁺¹    _up + q+2 _T

a (₄ + l)    a(q + l)^Jp’^q+l

(q y -1) ,

które pozwalają zwiększyć wykładnik p lub 9 o jedność, jeśli tylko suma p + q jest różna od —1.

Rozwiązując te równości względem    J_p,_q+_t i zastępując p i q odpowiednio

przez p —1 i q— 1 otrzymujemy wzory

(HI)

_T (a + hz)^pz⁸⁺¹    ap _T

~    p + q +1    ⁺ p + 4 + 1 ^P~¹'^q

(p + q ^ -1) ,

(a + bz)^pJrlz⁹    aq

~ ' b(p + q +1)    ~F(p + q + l) ^M-¹ •

(IV)