0056

58

VIII. Funkcja pierwotna (całka nieoznaczona)

zbadać przypadek, gdy również 4q’—p'² > 0. Wówczas q > 0, q' > 0 i 4\' qq' > pp' i mamy po kolei (')

[2(q+q')~PP'Y > \¹Vąti-PP’Y =

= (4?-p²)(4«'-p'²) + 4 (pVq'-p' \tq )² > (4q-p²)(4q'- p’²).

Tutaj dwa razy występuje znak nierówności słabej, ale równość nie może mieć miejsca w obu wypadkach jednocześnie: jeśli q ^ q\ to równość na pewno nie zachodzi w pierwszym przypadku, jeśli zaś q = q', to na pewno nie zachodzi w drugim. Tak więc nierówność (14¹), a wraz z nią (14), została udowodniona.

Wykonując podstawienie, przekształcimy całkę do postaci

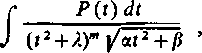
gdzie P (r) jest wielomianem stopnia 2m— 1, a A > 0. Stosując znowu (dla m > 1) rozkład ułamka właściwego

P{t)

(t² + k)^m

na ułamki proste dojdziemy do sumy całek postaci

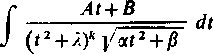
(k = 1, 2,..., m).

W szczególnym przypadku, gdy p = p', redukcję wyrażeń stopnia pierwszego osiągamy jeszcze prościej — przez podstawienie x = t—pjl, i bezpośrednio dochodzimy do całki o wskazanej przed chwilą postaci.

Otrzymana całka rozkłada się w sposób naturalny na dwie:

Ar    cc t dt    r    dt

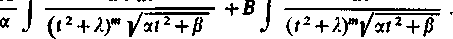
Pierwszą z nich można łatwo obliczyć stosując podstawienie u = \/at²+f}. Do drugiej można zastosować znane nam już podstawienie Abela

a t

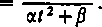
Na mocy (11) mamy

dt

du

/a r²+)S

a—u

2 >

1

Ponieważ --Ą— > ^qq'.