1036

Przykład 4.3. Przekrój wielośclanu płaszczyzną dowolną a daną prostą (/i_a) i punktem A

Na rysunku 65 przedstawiono rozwiązanie zadania metodą transformacji płaszczyzny przecinającą bryłę do położenia rzutującego.

Inna metoda rozwiązywania zadań, w których szukamy przekroju wielościa-nu dowolną płaszczyzną daną śladami, polega na wykorzystaniu rzutującego położenia ścian bryły przecinanej. Warunkiem niezbędnym jest występowanie takich ścian bryły przecinanej wynikające z jej położenia względem układu odniesienia.

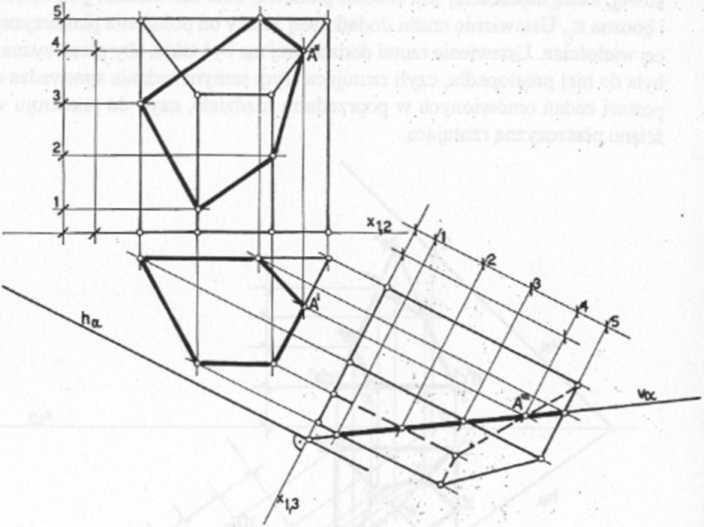
• Rys. 65

4.6. Metoda bezpośrednia wykorzystująca rzutujące położenie ścian przecinanego wiclościanu

Przykład 4.4. Przekrój płaszczyzną dowolną a daną śladami (v_Q, hj

a) Przykład przedstawia zastosowanie metody wykorzystującej rzutujące położenie ścian bryły przecinanej płaszczyzną dowolną a daną śladami (v^ hj (rys. 66a).

b)    Przekrój ściany (A, D, W) ostrosłupa jest odcinkiem (1,2) krawędzi przekroju płaszczyzny dowolnej a z płaszczyzną rzutującą e{y_e h_£) poprowadzoną przez ścianę (A, D, W) (rys. 66b).

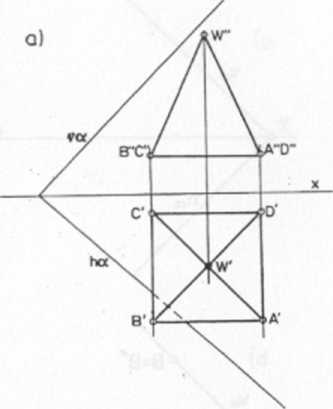
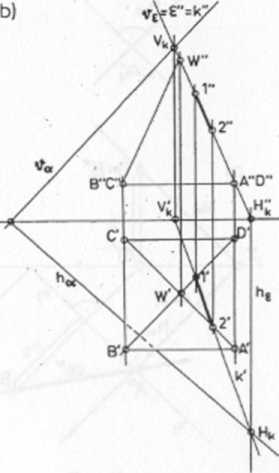
c)    Przekrój ściany (A, B, C, D) stanowiącej podstawę ostrosłupa wykorzystuje to, że leży ona w płaszczyźnie pionowo rzutującej prostopadłej do płaszczyzny a równoległej do rzutni poziomej n_y Rzut poziomy krawędzi przecięcia płaszczyzny f, z płaszczyzną przecinającą ostrosłup a jest równoległy do śladu poziomego płaszczyzny a(hj. Wynikiem operacji jest odcinek (3, 4) będący krawędzią przekroju podstawy ostrosłupa płaszczyzną a (rys. 66c).

d)    Przekrój ściany (B, C, fV) ostrosłupa jest odcinkiem (4, 5) krawędzi przekroju płaszczyzny dowolnej a z płaszczyzną rzutującą pionowo £^(^vfi, h₍) poprowadzoną przez ścianę (B, C,W) (rys. 66d).

e)    Pełny przekrój ostrosłupa (A, B, C, D_t W) płaszczyzną dowolną a otrzymano przez połączenie punktów (2) z (3) oraz (1) z (5), stanowiących krawędzie przecięcia pozostałych dwóch ścian ostrosłupa kolejno (A, B, W) oraz (C,D, W).

Na rysunku 66(a, b, c, d, e) pokazano przekrój płaszczyzną dowolną a. ostrosłupa, którego trzy ściany: podstawa (A, B, C, D) oraz trójkątne ściany

73