1033

4.1. Przekroje dowolną płaszczyzną daną śladami

Przekrój wielościanu płaszczyzną daną śladami można uzyskać różnymi metodami. Jedną z nich jest tzw. transformacja.

4.2. Przekształcenie układu odniesienia - transformacja

Obierzmy w układzie 3 rzutni Mongc’a n_v TTj, dodatkową płaszczyznę n_Ą, prostopadłą do rzutni n_]t lecz dowolnie usytuowaną względem (rys. 59).

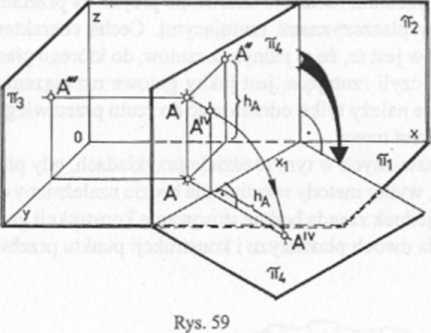
Płasztzyznę n_A nazywamy rzutnią dodatkową lub płaszczyzną transformacji. Płaszczyzna transformacji n_A przecina rzutnię poziomą 7T, w nowej osi rzutów x_r Rzut punktu A na płaszczyznę n_A jest rzutem równoległym prostokątnym, stąd - sprowadzając płaszczyzny n_]t n₂, n_Ą do położenia współpłaszczy-znowego (rys. 59), konstruujemy rzut dodatkowy punktu A przez narysowanie prostej odnoszącej przez jego rzut poziomy A' i prostopadłej do osi rzutów x, oraz odmierzenie na tej odnoszącej wysokości punktu A nad podstawą n_y Przykładem zastosowania podanej konstrukcji użycia płaszczyzny transformacji jest między innymi: rzut dodatkowy wielościanu oraz sprowadzenie płaszczyzny dowolnej do położenia rzutującego.

4.3. Dodatkowy rzut wielościanu

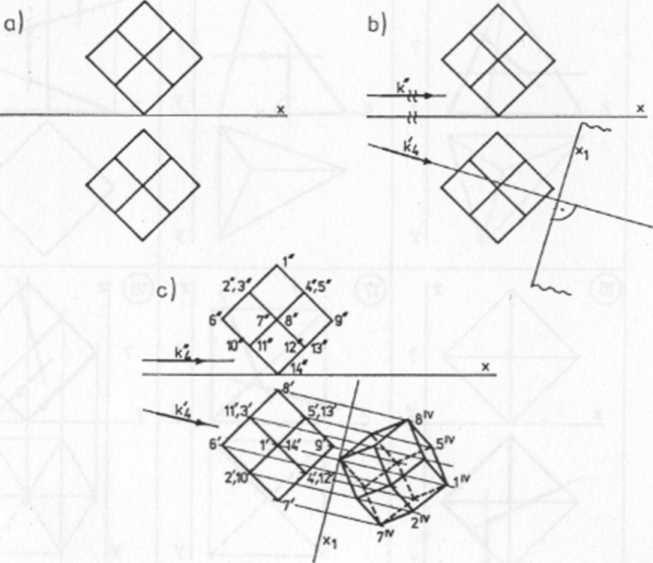
Obierzmy w układzie dwóch rzutni Monge’a tt, i ^ obraz dwunastościanu rombowego (rys. 60).

Ze wzglądu na cztery ściany wielościanu leżące w płaszczyznach poziomo rzutujących i cztery inne - pionowo rzutujące - trudne jest odczytanie kształtu tego wielościanu.

Wprowadźmy rzut dodatkowy na rzutnią n_v prostopadłą do rzutni poziomej n_x w taki sposób, aby kierunek rzutowania nie był zgodny z kierunkami osi x_%y,

z/np-M^OO-ys. 60b):

- przyjmując kierunek rzutowania k_A (k_A, k ₄"), wykreślamy nową oś rzutów x_{ prostopadle do k_Ą\

Rys. 60

67