1032

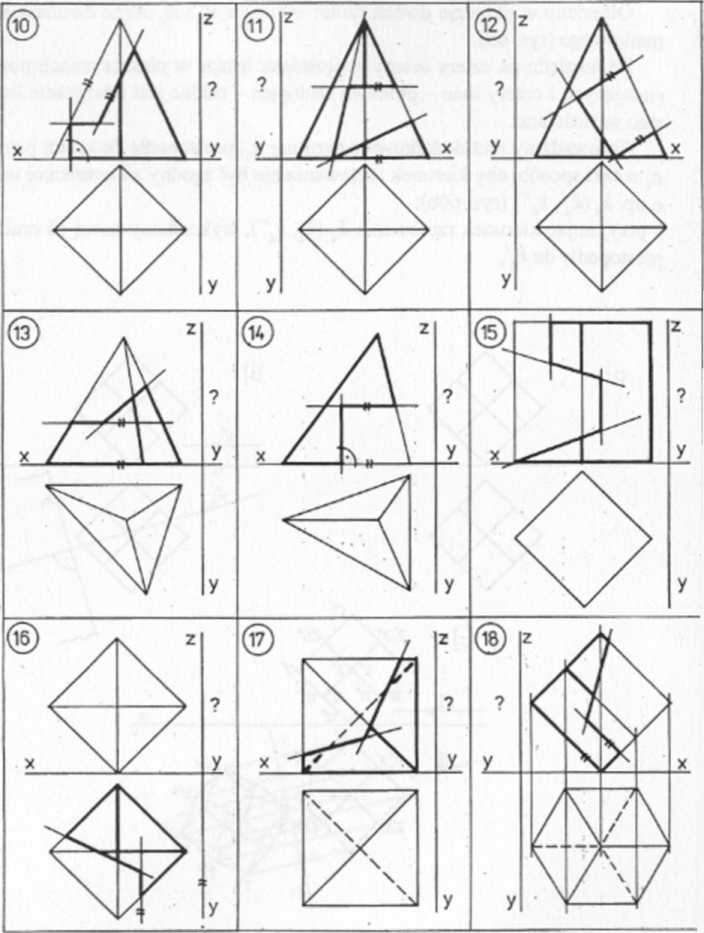
4. PRZEKROJE WIELOŚCIANÓW DOWOLNĄ PŁASZCZYZNĄ DANĄ RÓŻNYMI ELEMENTAMI

W poprzednim rozdziale omówiono przykłady przecinania wieloboków i wie-lościanów płaszczyznami rzutującymi. Cechą charakterystyczną tego rodzaju przekrojów jest to, że w jednym z rzutów, do którego płaszczyzna tnąca jest prostopadła, czyli rzutująca, jest jakby gotowe rozwiązanie. Punkty oznaczone w tym rzucie należy tylko odrzutować do rzutu przeciwległego lub dodatkowo narysować rzut trzeci.

W omawianych w tym rozdziale przykładach, gdy płaszczyzna tnąca ma być dowolna, wybór metody rozwiązania będzie uzależniony od danych wyjściowych. Główną jednak zasadą będzie stosowanie konstrukcji geometrycznych krawędzi przecięcia dwóch płaszczyzn i konstrukcji punktu przebicia prostą płaszczyzny.

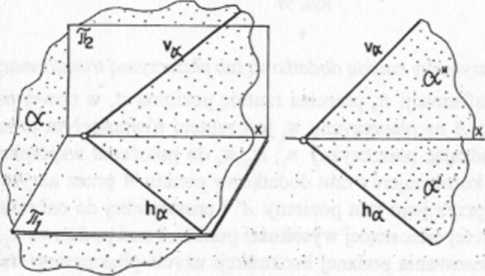
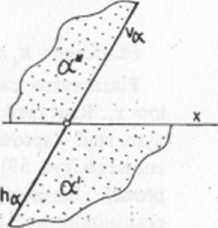
Rys. 58. Aksonometria i rzuty części dowolnej płaszczyzny z 1/4 przestrzeni oraz jej ślady pionowe (vj i poziome (AJ

65