1088

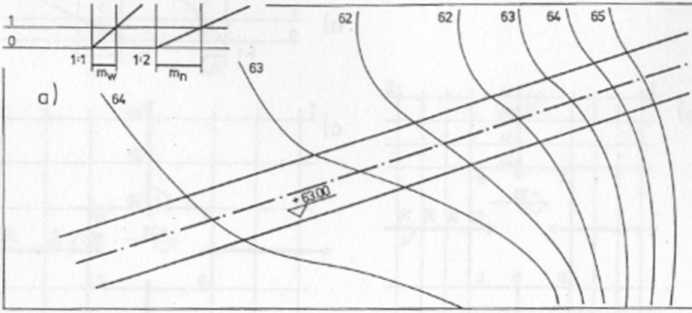
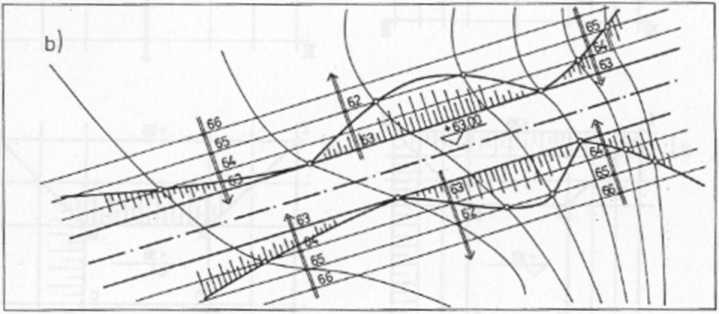
Rys. 177

Krawędzie drogi (poziome, na wysokości +63 m n.p.m.) przecinają się z war-stwicami terenu +63 w punktach rozgraniczających płaszczyzny wykopów i nasypów.

Ponieważ krawędzie drogi (pomijamy tutaj pobocze, rowy itp.) są poziome, proste spadu płaszczyzn wykopów i nasypów wychodzące z tych krawędzi są do nich prostopadłe w rzucie, lecz o przeciwnych zwrotach (rys. 177b).

Mając ustalone moduły m_w i m_n (rys. 177b), odkładamy je odpowiednio na prostych spadu i rysujemy warstwice płaszczyzn wykopów i nasypów.

Przykład 133

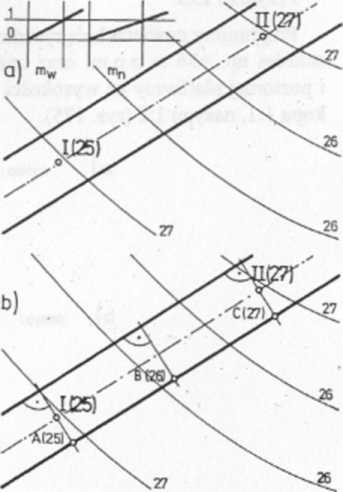
a)    W terenie o danym planie war-stwicowym (rys. 178a) naniesiono rzut projektowanej drogi o kącie nachylenia ustalonym punktami 1(25) i 11(27).

Wykreślić rzuty płaszczyzn nasypów i wykopów o danych modułach.

b)    Ponieważ krawędzie boczne drogi są pochyłe, więc proste spadu płaszczyzn nasypów i wykopów nie są do nich prostopadłe, a warstwice równoległe.

Określmy cechy punktów A(25) i C(27) na krawędzi drogi i zestopniuj-my ją, uzyskując punkty: A(25), £(26), C(27) (rys. 178b).

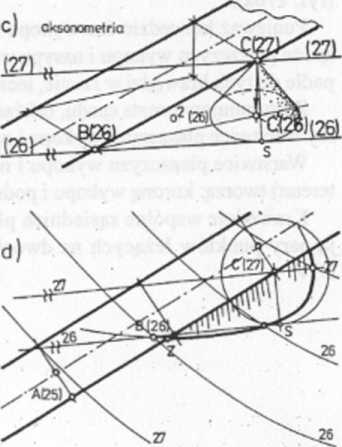
c,d) Wybierzmy parę punktów sąsiednich, np. £(26) i C(27), a z nich punkt wyższy, tzn. punkt C. Rzutujmy pionowo punkt C na poziom punktu £(26). Punkt C będzie środkiem okręgn o promieniu r_t = m_n. Okrąg ten jest podstawą stożka obrotowego o wierzchołku C(27), którego tworzące są nachylone pod tym samym kątem do poziomu co płaszczyzna nasypu (rys. 178c i d).

Jeżeli z punktu £(26) narysujemy styczną do okręgu o\26), otrzymamy poziomą prostą o wysokości (26), a zatem warstwicę płaszczyzny nasypu. Dalsze warstwice otrzymamy rysując przez punkty A(25) i C(27) krawędzi drogi proste równoległe do warstwicy (26).

Następnie szukamy punktów wspólnych powierzchni terenu i płaszczyzny

177