1089

3N 4 * 3(AT-H) 4    ’

gdy N jest parzyste gdy N jest nieparzyste

(4.18)

Przykład 4.18.

Na podstawie danych z przykładu 4.15 oblicz, ile wynosi kwartyl pierwszy i kwartyl trzeci wyników z tej klasówki?

Rozwiązanie

Sposób wyznaczania Q, i Q₃ jest analogiczny do sposobu wyznaczania mediany. Wykorzystamy w tym celu utworzoną w przykładzie 4.15 tabl. 4.12, gdzie wyznaczyliśmy częstości absolutne skumulowane.

Kolejnym krokiem przy wyznaczaniu kwartyli jest obliczenie ich numerów, korzystając ze wzorów 4.17 i 4.18:

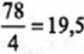
i Afc=M±I> ₌ 3<*±*>

4    4    4    4    4

Kwartyl znajduje się w klasie, w której skumulowane częstości przekraczają lub osiągają co najmniej numer kolejny kwartyła. W naszym przykładzie numer kwartyla pierwszego wynosi 6,5. Jednostki o tym numerze leżą w trzeciej klasie, stąd Q, = 3. Z kolei numer kwartyla trzeciego wynosi 19,5. Jednostki o tym numerze leżą w piątej klasie, stąd Q₃ = 4.

Dwadzieścia pięć procent uczniów w klasie Ila z klasówki ze statystyki otrzymało ocenę dostateczną lub niższą, a 75% procent uczniów ocenę dostateczną lub wyższą (interpretacja Q,)- Siedemdziesiąt pięć procent uczniów tej klasy otrzymało z klasówki oceną dobrą lub niższą, a 25% ocenę dobrą lub wyższą (interpretacja Q₃).

W przypadku materiału statystycznego przedstawionego w postaci szeregów rozdzielczych z przedziałami klasowymi Q, i Q₃ obliczamy, podobnie jak medianę, korzystając ze wzorów interpolacyjnych:

Q\~^xq. ^+ ty^rQx “ *W-1 )>	(4.19)
^nn.	(4.20)

gdzie:

^XQ

^hQ

ⁿQ

ⁿuk- 1

Nr_Q

-    dolna granica przedziału klasowego, który zawiera dany kwartyl,

-    rozpiętość przedziału kwartyla,

-    częstość odpowiadająca przedziałowi klasowemu, w którym znajduje się kwartyl,

-    częstość skumulowana przedziału poprzedzającego przedział, w którym znajduje się szukany kwartyl,

-    numer kwartyla.

Przykład 4.19.

Na podstawie danych z przykładu 4.16 wyznacz kwartyl pierwszy i kwartyl trzeci wydaj pości pracy pracowników w tym przedsiębiorstwie.

Rozwiązanie

Do wyznaczenia kwartyla pierwszego i trzeciego wykorzystamy wzory interpolacyjne 4.19 i 4.20. Sposób ich wyznaczania jest analogiczny do sposobu wyznaczania mediany, dlatego wykorzystamy utworzoną w przykładzie 4.16 tabl. 4.13. gdzie wyznaczyliśmy częstości absolutne skumulowane. Następnie obliczamy numery kwartyłi korzystając ze wzo-rów4.17 i 4.18:

^Nr*⁼ T⁼¹?⁼³³

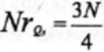
3 132 4

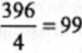
Zatem kwartyl pierwszy znajduje się w trzecim przedziale klasowym, a kwartyl trzeci w czwartym przedziale klasowym. Przystępujemy zatem do obliczenia wartości kwartyłi korzystając ze wzorów interpolacyjnych. I tak:

2, =*_a +—K    6 + ^—(33-30)= 6 + ^-*3 = 6 + 0,16 = 6,16,

Q> =*a⁺—K,-'W-.)=⁸⁺^(⁹⁹ - ⁶⁷)=⁸+A-³²=⁸⁺¹.⁴²=⁹.⁴²-

45    45

Kwartyl pierwszy wydajności pracy w tym przedsiębiorstwie wynosi 6,16, co oznacza, że 1/4 pracowników tego przedsiębiorstwa ma wydajność pracy wynoszącą 6,16 szt./godz. lub mniej, a 3/4 pracowników ma wydajność pracy wynoszącą 6.16 szt./godz. lub więcej. Kwartyl trzeci wydajności pracy w tym przedsiębiorstwie wynosi 9,42, co oznacza, że 3/4 pracowników tego przedsiębiorstwa ma wydajność pracy wynoszącą 9,42 szt./godz. lub mniej, a 1/4 pracowników ma wydajność pracy wynoszącą 9,42 szt./godz. lub więcej.

Należy zauważyć, że znajomość wartości Q, i Q₃ w uporządkowanymi szeregu pozwala nam powiedzieć, że połowa (50%) jednostek danej zbiorowości statystycznej przyjmuje wartość od Q, do Q₃:

-t-

Jeżeli zbiorowość jest bardzo liczna, może się okazać, że podział zbiorowości na ćwiartki jest niewystarczający. Stosujemy wówczas decyle (dzielące zbiorowość na subpopulacje dziesięcioprocentowe) lub percentyle (dzielące zbiorowość na sub-populacjc jcdnoprocentowe). Sposób obliczania tych miar statystycznych jest analogiczny jak w przypadku kwartyłi.

117