1098

Z obliczonych wartości wynika, że w klasie A liczba błędów popełnionych w dyktandzie odchyla się przeciętnie od średniej arytmetycznej (x = 4 błędy) o 0.7 błędu. Natomiast w klasie B przeciętne odchylenie od średniej jest większe i wynosi 2,12 błędów. Odchylenie standardowe oraz wcześniej obliczone odchylenie przeciętne prowadzą do wspólnego wniosku, że uczniowie klasy B są bardziej zróżnicowani pod względem liczby popełnionych w dyktandzie błędów.

Widzimy, żc wartość poznawcza odchylenia standardowego i przeciętnego jest taka sama, występuje jednak różnica w wielkości uzyskanych wyników. Dla tych samych danych zachodzi następujący związek: d_x < S_x. Różnica ta jest efektem innego sposobu obliczania tych miar. Odchylenie standardowe jest miarą bardziej dokładną.

Przykład 5.5.

Właścicielka salonu fryzjerskiego Paloma dokonała oceny funkcjonowania placówki w czerwcu 2004 roku. Analizowała m.in. liczbę klientek korzystających z usług salonu w poszczególnych dniach czerwca 2004 roku. Zebrane informacje zostały przedstawione w szeregu postaci:

Tablica 5.5. Rozkład liczby klientek salonu Paloma

Liczba kobiet dziennie korzystających z usług salonu Paloma	Liczba dni
10	1
11	3
14	7
15	8
18	3
20	3

Źródło: dane umowne.

Wyznaczmy wartość odchylenia standardowego liczby pań korzystających w poszczególnych dniach czerwca 2004 roku z usług salonu fryzjerskiego Paloma.

Informacje o wartościach cechy jednostek badanej zbiorowości zostały przedstawione w szeregu punktowym, wartość odchylenia standardowego obliczamy zgodnie ze wzorem

5.6.

Stosujemy w tym przypadku następujący schemat obliczeniowy:

1)    obliczamy średnią arytmetyczną (*);

2)    wyznaczamy odchylenia, tzn. od poszczególnych wartości cechy odejmujemy średnią arytmetyczną (* ~ *) ;

3)    obliczamy kwadraty odchyleń wyznaczonych w 2 punkcie (x_t - .r)^:;

4)    obliczamy iloczyny, mnożąc kwadraty odchyleń (x,-x)² przez liczebność (n) odpowiednich klas (a:, -x)²n,;

5)    dodajemy uzyskane wcześniej iloczyny Ś (*<“*) ⁿh

6)    obliczoną sumę iloczynów £(*,-*)*«, dzielimy przez liczebność zbiorowo-

r

N

Ści (;V)

7) wyciągamy pierwiastek kwadratowy z ilorazu otrzymanego w punkcie 6)

JUJ-

JV

Obliczenia dokonane zgodnie z powyższym schematem prezentuje tablica 5.6.

Tablica 5.6. Obliczenia pomocnicze do przykładu

Liczba kobiet dziennie korzystających z usług salonu Paloma x,	Liczba dni	W	xt-x	(xi-xy	(x,-x)^2n,
10	1	10	-5	25	25
11	3	33	-4	16	48
14	7	98	-1	1	7
15	8	120	0	0	0
18	3	54	3	9	27
20	3	60	5	25	75
Razem	25	375	X	X	182

Źródło: obliczenia własne.

Obliczenie średniej arytmetycznej wymaga podstawienia do wzoru:

k

5>a ₃₇₅

x = ^-= — = 15 kobiet

N 25

Średnio dziennie w czeiwcu 2004 roku 15 kobiet korzystało z usług salonu Palcma. Następnie, korzystając z obliczeń zawartych w tablicy 5.6 wyznaczamy odchylenie standardowe:

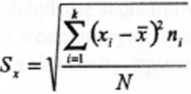
fi82

V 25

2,7 kobiet.

135