122

Pr złócc J**l red pruł dr lubJ K. PtirownlcKgo"Podstawy tuksyfculągii*. 'K\«r«.r*i 3006. ISBN k.V->i;h-.ł|>2 0 C by WNT

Obecnie obliczenia kinetyczne nie sprawiają trudności. Powszechna dostępność komputerów wyposażonych w program lL\CliL umożliwia natychmiastowe obliczenie parametrów kinetycznych dla reakcji 1 rzędu Łatwo dostępny program OR1GIN 5.0 jest szczególnie dogodny do obliczeń kinetycznych, gdyż umożliwia m in obliczanie parametrów kinetycznych dla reakcji ri-tcgo rzędu (n > 1 h modeli wicloprzedzialowych (dopasowywanie parametrów funkcji wielowykładniczych do wyników doświadczalnych oraz obliczanie błędów względnych tych parametrów!, jak również wykonywanie wykresów z zaznaczonym błędem obliczeń

5.2.2. Model jednoprzedziałowy otwarty

Jest to najprostszy model kinetyczny. Jeżeli do ustroju, tzn. do przedziału szyhkowyntiennego A, wprowadzi się jednorazowo substancję S wydalającą się tylko jedna droga li <np. z moczem) ze stała szybkości k_h to sytuację taka obrazuje schemat

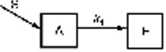
Model jednoprzedziałowy bywa stosowany głównie dla substancji dobrze rozpuszczalnych w wodzie i nie odkładających się w tkance tłuszczowej. Zwykle przedział ten obejmuje wtedy nic tylko osocze krwi, ale i inne płyny pozakumórkowc (u dorosłego człowieka o objętości 15 dm’). a często również bogate w wodę płyny zewnątrz- i wewnątrzkomórkowe. Przykładem mogą tu być alkohole niższe, które rozmieszczają się w tkankach ustroju proporcjonalnie do zawaitości w nich wody.

W modelu jcdnoprzcdziałowym otwartym zakłada stę. żc substancja obca nie ulega żadnej przemianie (biotransformacji) w ustroju Jedynym czynnikiem powodującym obniżenie jej poziomu jest wydalanie, które zachodzi tylko jedną drogą, najczęściej z moczem, Szukając właściw ej funkcji matematycznej opisującej ubytek substancji z ustroju, przyjmuje się. żc wydalanie jest procesem I rzędu. tzn. szybkość wydalania jest wprost proporcjonalna do stężenia substancji w przedziale A, co wyraża równanie: gdzie: [S_A] - zawartość substancji S w przedziale A, mg, rt, - siata wydala ma. h t - czas. h.

Rozwiązanie równania (4) ma postać:

<5!

[Sa], = [SaIuC"*-'

gdzie: c podstawa logarytmów naturalnych, c 3: 2,72, [S^Jo początkowa zawartość substancji w ustroju dla t — 0: [Sa], zawartość substancji w ustroju po czasie i.

122    5. KINETYKA PRZEMIAN I WYDALANIA SUBSTANCJI TOKSYCZNYCH