0076

78

VIII. Funkcja pierwotna (cdka nieoznaczona)

/

dz

(1+hz²) V(T~z²) (1 ~k²z²)

(0 < k < 1)

(ostatnią z nich otrzymujemy z H₁ wprowadzając zamiast a / 0 nowy parametr k = ——).

a

Całek tych, jak pokazał LiouviIle, nie można już wyrazić w postaci skończonej przez funkcje elementarne. Legendre nazwał je całkami eliptycznymi odpowiednio pierwszego, drugiego i trzeciego rodzaju. Pierwsze dwie z nich zawierają tylko jeden parametr k, ostatnia zawiera oprócz tego parametru jeszcze parametr zespolony h.

Legendre uprościł te całki jeszcze bardziej, wykonując w nich podstawienie z = sin p (p zmienia się od 0 doyn)-Po tym podstawieniu pierwsza z tych całek przyjmuje postać

(11)

/

d<p

^1—fc²sin² <p

Druga przekształca się w sposób następujący:

/

sin²p dtp y/l—k²sin² <p

1 ę dtp

k² J ]/l-k²sin²p

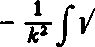
1 —fc²sin² <p dtp,

tzn. sprowadza się do poprzedniej całki i do nowej całki

(12)    J |/l—k²sin^a tp dtp.

Wreszcie trzecia całka przechodzi przy powyższym podstawieniu w całkę

(13)

/

_dtp_

(1 + h sin² p) ]/1—k²sin^a tp

Całki (11), (12) i (13) nazywają się także całkami eliptycznymi pierwszego, drugiego i trzeciego rodzaju w postaci Legendre'a.

Szczególnie ważne i często używane są dwie pierwsze z nich. Jeśli uważać, że całki te znikają dla p = 0 i ustalić w ten sposób zawarte w nich stałe dowolne, to otrzymamy dwie zupełnie określone funkcje zmiennej p, które Legendre oznaczył odpowiednio przez F(k, tp) i E(k,tp). Wskazany jest tutaj oprócz zmiennej niezależnej tp także występujący w całce parametr k, zwany modułem.

Legendre ułożył obszerne wartości tablice tych funkcji dla różnych p i różnych k. W tablicach tych nie tylko argument p jest traktowany jako kąt i wyrażony w stopniach, lecz także moduł k (ułamek właściwy!) jest traktowany jako sinus pewnego kąta 0, który to kąt podaje się w tablicach zamiast modułu, i to również w stopniach.

Oprócz tego Legendre, a także i inni uczeni zbadali bardzo głębokie własności tych funkcji, wyprowadzili dla nich wiele wzorów itd. Dzięki temu funkcje F i E Legendre’a weszły w zakres funkcji, które spotykamy w analizie i jej zastosowaniach, na równi z funkcjami elementarnymi.