Image0086 BMP

fi iy z;im u suwaniu wzoru

fch C x + j y) j = Vi (eh 2x -t- cos 2y)

otrzymujemy w wyniku

(9-53)

trrJlb f⁺“g

Łatwo sprawdzić, że dla rzeczywistych x jest ch x+cos x^2. Istotnie, rozwijając obie funkcje w szeregi potęgowe, mamy

x² x⁴

x² x⁴

chx+cosx=l +-—H----K.. + 1----+ „

2!    4!    2!    4

⁴    „ J*^Ą \

r+--2+2^—

bowiem wyrażenie w nawiasie jest nieujemne, a znak równości otrzymuje się dla x=0.

Wnioskujemy stąd, źe ^/y ^ch^+cos1, wobec czego J_mm>    Oznacza

to, że na wewnętrznej powierzchni każdej płyty gęstość prądu jest większa niż na zewnętrznej powierzchni.

Rozkład gęstości prądu w każdej płycie charakteryzuje wyrażenie

= |ch k (b + d ± y)J,

''zewm

przy czym znak plus dotyczy lewej płyty, a znak minus - prawej płyty. Wykres tej zależności przedstawia rys. 9.6. Rozkład gęstości prądu w obu płytach jest symetryczny. Z powyższych rozważań wynika, że przepływ prądu w jednej płycie wywiera wpływ na rozkład prądu w drugiej płycie. Zjawisko to nosi nazwę zjawiska zbliżenia.

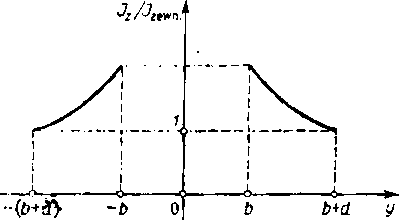
Rys. 9,6. Rozkład gęstości prądu w płytach przedstawionych na rys. 9.5

9.5. Przewody w żłobka maszyny elektrycznej

Rysunek 9.7 przedstawia w sposób ideowy n jednakowych przewodów o przekroju prostokątnym, umieszczonych w żłobku maszyny elektrycznej. Zakładamy, że w każdym przewodzie płynie taki sam prąd o wartości zespolonej /, a y oraz fi są konduktywnośdą

era/ pr/.cniknlnn(i'ii| magnetyczni] przewodu. Nictli u oraz h n/mic/ają odpowiednio szerokość oruz wysokość każdego przewodu. Zakładamy. że grubość izolacji pi/rwodów jest pomijatnie mała. Wprowadzamy układ współrzędnych prostokątnych i, i. ;. jak to pokazano na rys. 9.7. Przyjmujemy, że w każdym przewodzie prąd płynie w kierunku

²t

	1 '	|
	Azjj Ó	r	— "	I/**
n	Z' T
	i ;				i X
				i i	h
n-1			®	:.;!j	t
	1 ■ I 1 i.S ^1' i			>: i !
Z	\%	®	©j
1	k	®	.1	# m I;
	[>/: \ \	U-	3	t ł s

Rys. N.9.7. Przewody umieszczone w żłobku maszyny elektrycznej

osi 0i\ W tych warunkach linie prądowe są równoległe do osi Oy, wobec czego gęstość prądu oraz natężenie pola elektrycznego mają tylko składowe J_y oraz E_y, niezależne od współrzędnej y. Zakładamy ponadto, że składowe J_yi E_r nie zależą również od zmiennej .t, wobec tego są one funkcjami jednej zmiennej z, czyli J_y(z) oraz £„(z).

Na podstawie II równania Maxwella stwierdzamy po wykonaniu prostych przekształceń, że natężenie pola magnetycznego ma tylko składową HJz) i znajdujemy

If_x

1 d E, jtDfl dz

(9.54)

W celu otrzymania drugiego równania rozpatrzymy prostokąt o wysokości A: (rys. 9.7). Napięcie magnetyczne wzdłuż obwodu tego prostokąta równa się a[ff_x(z + Az) — - //_T(z)], przy pominięciu dążącej do zera jego wartości wzdłuż boku Az, zaś prąd przepływający przez wnętrze tego prostokąta jest równy J/iAz, wobec czego zgodnie z prawem przepływu mamy

u [//_X(z+Az)- H_x{zj]^J_y a Az ,

czyli

H_x(z + Az) -//,(=) Az