Image0039 BMP

każdym punkcie rozpatrywanego obszaru. Istotnie dla ;j»consl na podutawie wzoru vB=0 otrzymujemy divll~0, a po podstawieniu zależności (4.11), mamy

div grad F₍₎=0,

:yli równanie (4.13).

3.2. Potencjał wektorowy

Obliczanie pól magnetycznych prowadzi do rozwiązania równań różniczkowych tąstkowych

rotH=J, divB=0.

(4.14)

(4.15)

! wielu przypadkach obliczenia upraszczają się po wprowadzeniu funkcji wektorowej nazywanej potencjałem wektorowym.

Potencja) wektorowy określamy za pomocą wzoru

B=rotA.

(4-16)

otencjał wektorowy jest funkcją opisującą pole magnetyczne, bowiem jej znajomość

możliwia wyznaczenie indukcji magnetycznej. Należy zwrócić uwagę, że spełnione jest

ównanie (4.15), ze względu na tożsamość wektorową divrotA=0.

Podane określenie potencjału wektorowego nie jest jednoznaczne, bowiem istnieją iżne wektory, dające tę samą indukcję magnetyczną. Na przykład dla każdego z wek->rów A oraz A+grad ę, gdzie ę jest dowolną różniczkowalną funkcją skalarną, otrzymuje się B=rot A, ze względu na zależność wektorową rot grad <p—0. W celu uzyskania jdnoznacznej definicji potencjału wektorowego (z dokładnością do stałej) przyjmiemy rarunek dodatkowy o postaci

div A«0.

(4.17)

Rozpatrzmy pole magnetyczne w środowisku jednorodnym (^=const). Na pod-tawie równania rot H-J otrzymujemy

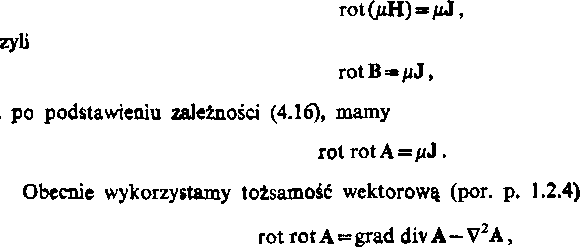
;dzie: V^aA jest laplasjanem wektora A i uwzględnimy warunek (4.17); otrzymujemy w wy-iku równanie

Potencjał wektorowy spełnia wektorowe równanie Polssona, która w układzie wapół-

rpilnych prostokątnych równoważne jest trzem równaniom skalarnym Potisona dla

poszczególnych składowych, czyli

(4.19)

V²A_x=-iU_x, V²j4_z= —fiJ_z ■

Rozwiązanie podstawowe równania Poissona (4.18) wyraża się wzorem

A(x

J(x\ y',z')

dx'dy'dz\

(4.20)

który można otrzymać przez analogię do zależności (2.32). Wielkość /■=* - v'(A-x^r)³+(j'-y)² + (z-z')² w tym wyrażeniu oznacza odległość punktu źródłowego (a'. y\ z') od punktu obserwacji (x, y, z), a obszarem v całkowania jest cały obszar objęty przepływem prądu (rys. 4.6).

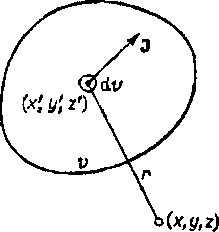
Rys. 4.6. Wyjaśnienie oznaczeń występujących we wzorze (4.20)

Na zewnątrz obszaru v, gdzie J — 0, potencjał wektorowy (4.20) spełnia równanie 1 ap)ace'a    _a

V²A=0.    (4.21)*

W wielu przypadkach przepływ prądu występuje w cienkich przewodach. W tych warunkach mamy (por. rys. 4.7)

Jdr—idl,    (4.22)

dl

Rys. 4.7. Elementarny odcinek przewodu