Image0021 BMP

W charakterze przykładu obliczymy potencjał ładunku w punkcie P odległym o t od odosobnionego ładunku punktowego Q, umieszczonego w jednorodnym środowisku o pneenikałności elektrycznej r.. Przyjmiemy, że potencjał punktu w nieskończoności równy jest zeru. Całkując wzdłuż linii pola przechodzącej przez punkt P (rys. 2.1), mamy

Vp— ffidr,

P

zgodnie ze wzorem (2.14), a po podstawieniu zależności (2.6), otrzymujemy

(2.17)

^F 4xti J r² 4ner

2.2.3. Potencjał ładunku przestrzennego i powierzchniowego

wobec czego potencjał w punkcie P przedstawia wzór 4ne J r

p da wynosi

Niech p oznacza gęstość ładunku przestrzennego w obszarze v, a a - przenibainość elektryczną środowiska jednorodnego. Potencjał wytworzony w punkcie P przez ładunek pdi>

4wer

gdzie: r=-J(x— x')²+(y—/)³ + (z—z^r)¹ jest odległością między punktem obserwacji P o współrzędnych x,y,z a punktem wewnętrznym obszaru elementarnego dc o współrzędnych x', y', z\ zwanym często punktem źródłowym (rys. 2.3).

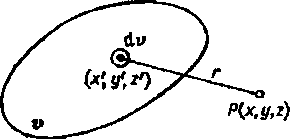
Rys. 2.3. Obszar zawierający ładunek przestrzenny

Ładunek elektryczny znajdujący się na powierzchni nazywamy ładunkiem powierzchniowym, a jego gęstość jest określona wzorem

Aq

<r= lim —

A5-*0 A o

(2.18)

gdzie: Aą jest ładunkiem znajdującym się na powierzchni elementarnej AS. Jednostką ładunku powierzchniowego jest kuloinb na metr kwadratowy (C/m²).

Ładunek powierzchniowy występuje w przypadku naładowanych ciał metalowych, bowiem ładunek jest rozłożony na powierzchni tych ciał. Potencjał wywołany w punkcie

/* prze/, ładunek powierzchniowy znajdujący się na powierzchni S ma postać':

V

1 r <rdS J r

(2.19)

gd/ic: r jest odległością punktu obserwacji od punktu źródłowego.

Punkty, w których potencjał V(ar, y, z) ma wartość stałą, położone są na powierzchni zwanej powierzchnią ekwipotencjalną. Powierzchnie ekwipotencjalne są przykładem powierzchni ekwiskalarnej (por. p. 1.2.1). Linie pola elektrycznego są ortogonalne względem powierzchni ek wipo tencjalny ch.

2.3. Warunki brzegowe. Prawo załamania

Wektory E i D muszą spełniać określone warunki brzegowe na powierzchni granicznej dwóch różnych środowisk.

Przypuśćmy, że na powierzchni granicznej dwóch dielektryków o przemkalnościach elektrycznych Ci i e₂ znajduje się ładunek powierzchniowy o gęstości a. Rozpatrzmy zamkniętą powierzchnię walcową umieszczoną w obu środowiskach w ten sposób, że podstawy dS są równoległa do powierzchni granicznej i znajdują się w różnych środowiskach (rys. 2.4). Niech 2)_ai oraz D„₂ oznaczają składowe normalne indukcji elektrycznej bardzo blisko powierzchni granicznej, odpowiednio w środowisku górnym i dolnym. Strumień

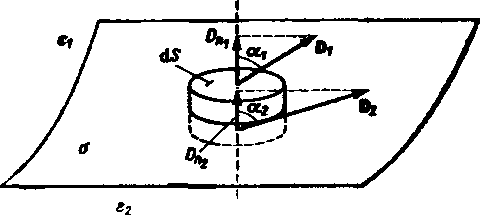
Rys. 2.4. Elementarna powierzchnia zamknięta przy powierzchni granicznej dwóch środowisk

elektryczny przez omawianą powierzchnię walcową wynosi D_nldS—D„₂dS, przy pominięciu strumienia przez powierzchnię boczną, który zanika, gdy wysokość walca dąży do zera. We wnętrzu tej powierzchni walcowej znajduje się ładunek ndS, wobec czego na podstawie twierdzenia Gaussa otrzymujemy

a stąd

D_nl dS—D_B2dS=odS,

D_mi — D_n2 — <7.

(2.20)

Jeżeli na powierzchni granicznej dwóch środowisk znajduje się ładunek powierzchniowy, lo składowa normalna wektora indukcji elektrycznej jest nieciągła w punktach tej powierzchni. Różnica tych składowych po obu stronach powierzchni granicznej równa się gęstości ładunku powierzchniowego.