Image0046 BMP

są łatwiej magncsowalii?. a indukcja magnetyczna w stanic nasyceniu irM większa dla tych ciał niż dla ciał twardych magnetycznie.

Gdy pętla hislerezy jest dostatecznie wąska, wówczas w obliczeniach można pominąć zjawisko liisterezy magnetycznej, posługując się jedynie krzywą magnesowania.

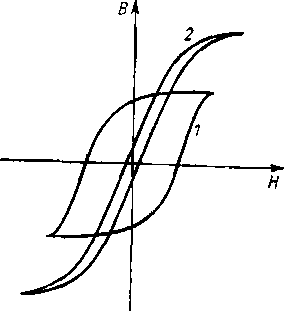
Rys. 4.17. Przykłady pętli histerezy 1 — ciała magnetycznie twarde,

2 — ciała magnetycznie miękkie

4.6.3. Przenikalność magnetyczna statyczna i dynamiczna

Gdy w uzwojeniu cewki płynie prąd stały, wówczas natężenie H w rdzeniu jest wielkością stałą, wobec czego pole magnetyczne jest niezmienne w czasie. Statyczną przeni-kalnością magnetyczną fi„ w punkcie A krzywej magnesowania nazywamy iloraz indukcji magnetycznej B przez natężenie H pola magnetycznego w tym punkcie, czyli

B\

_H\

(4.56)

A

Przenikalność magnetyczna statyczna jest proporcjonalna do tangensa kąta a, między sieczną 0A a osią OB (rys. 4.18).

Przenikalność magnetyczna statyczna nienasyconych ciał ferromagnetycznych jest znacznie większa od przenikainości magnetycznej próżni fj₀. Przedstawiając statyczną

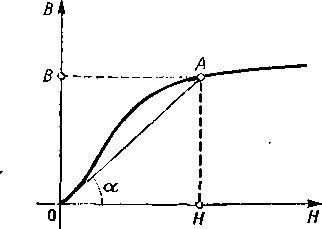
Rys. 4.18. Określenie statycznej prze-nikalności magnetycznej

I't /niikalnnść magnetyczną w postaci (t ji,, widzimy. że w przypadku nic nasyconych li:il ferromagnetycznych mamy /i,_u -I.

Przypuśćmy, żc w uzwojeniu rozpatrywanej cewki płynie prąd zmienny i. Ponieważ naiyżeriie // jest proporcjonalne do prąciu i, więc zmienia się ono w takt zmian prądu. W ulżeniu cewki istnieje wówczas zmienne pole magnetyczne. Załóżmy, żc prąd i zmienia mc w ten sposób, że natężenie pola magnetycznego zmienia się między wartościami H— Ali u If + Afl. Punkt krzywej magnesowania odpowiadający natężeniu pola magne-ueznego w rdzeniu przesuwa się zatem wzdłuż łuku A' A" krzywej magnesowania (rys. 4 l¹M (idy łuk A'A" jest dostatecznie krótki, wówczas możemy go zastąpić odcinkiem ślicznej in do krzywej magnesowania poprowadzonej przez punkt A.

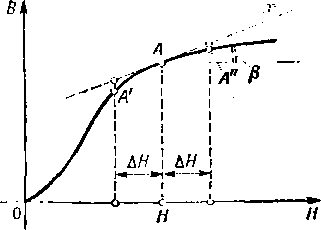
Rys. 4.19. Określenie dynamicznej przenika (ności magnetycznej

liyiiiwuczną przenikalnością magnetyczną fij w punkcie A krzywej magnesowania nazywamy wartość pochodnej indukcji magnetycznej B względem natężenia fi poła magu e licznego w tym punkcie, czyli

Pi =

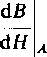
(4.57)

[ >>n,imic/na przenikalność magnetyczna ft_d jest proporcjonalna do tangensa kąta, iuki tworzy styczna m z osią OH (rys. 4.19).

Konieczność rozróżniania statycznej i dynamicznej przenikalności magnetycznej za-diud/i tylko w przypadku ciał ferromagnetycznych, bowiem zależność B—f (H) dla tych t uił icst nieliniowa.

4.7. Warunki brzegowe. Prawo załamania

obliczając strumień magnetyczny przez powierzchnię walcową jak na rys. 2.4, zauważamy podobnie jak w p. 2.3, przy uwzględnieniu wzoru (4.2), że składowa normalna¹ wiiinra indukcji magnetycznej jest ciągła w punktach powierzchni granicznej dwóch ■.lodowisk, wobec czego

B_nL=B_n2.    (4.5X1

1

¹1 / > puśćmy, że na powierzchni granicznej dwóch środowisk znajduje się bardzo iH-nka płyta, która w granicy staje się płaszczyzną przewodz.ącą, wzdłuż której płynie pnul Jeżeli pizepływ prądu ogranicza się tylko do samej powierzchni, to prąd taki