Image0064 BMP

Stwicul/nmy zatem, że indukcyjnióć wzajcmmi dwóch obwodów pi/edstawi.i w/ór

Stwicul/nmy zatem, że indukcyjnióć wzajcmmi dwóch obwodów pi/edstawi.i w/ór

<6.53)

Otrzymany wynik znany jest pod nazwą twierdzenia Neuman na.

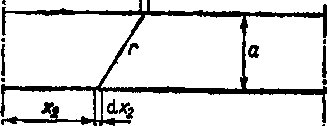
Jako przykład obliczymy indukcyjuość wzajemną dwóch równoległych przewodów o długości /, znajdujących się w środowisku o przenikalności magnetycznej ft_Q (rys. 6.14). Gdy zwroty prądów w obu przewodach są jednakowe, wówczas wektory dl, oraz dl₂ mają zwroty jednakowe, wobec czego dl, •dl₂=d.v₁d.r₂. Jeśli natomiast zwroty tych

i._a_

l

Rys. 6.14. Dwa równoległe przewody o długości skończonej

L

prądów są przeciwne, to dl₍-dl, = — d.v,d.v₂. Na podstawie wzoru (6.53) mamy zatem

I i

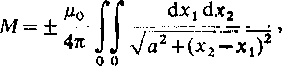
(6.54)

przy czym przyjmujemy znak plus, gdy prądy mają zwroty zgodne, a znak minus — gdy zwroty prądów są przeciwne.

Po wykonaniu całkowania otrzymujemy

M = +

a w przybliżeniu dla />a mamy

(6.56)

6.5.2. ludokcyjność wewnętrzna przewodu

Pole magnetyczne istnieje zarówno na zewnątrz przewodu jak i w jego wnętrzu. Strumień skojarzony przewodu można podzielić na strumień skojarzony wewnętrzny oraz zewnętrzny y/_s. W związku 2 tym rozpatruje się indukcyjność wewnętrzną przewodu

oni/ indukcyjne^ zewnętrzną

i-,-

/

(6.58)

udzie i oznacza prąd płynący w przewodzie.

Obliczymy obecnie indukcyjność wewnętrzną przewodu. Indukcyjność zewnętrzną przewodu wyznaczymy w p. 6.5.3.

Rozpatrzymy przewód o przekroju kołowym (rys. 6.15), wykonany z materiału nie-ferromagnetycznego o przenikalności magnetycznej {i. Natężenie pola magnetycznego

IX

2 nti

wewnątrz przewodu w odległości x od jego osi wynosi    (por. p. 4.2.2). Rozlo-

iymy przewód na elementarne obszary o postaci wydrążonych walców o wysokości / i o podstawie w kształcie pierścienia, którego promieniami są x oraz jc+dje (rys. 6.15).

Rys. 6.15. Przekrój poprzeczny przewodu

Ponieważ gęstość energii pola magnetycznego wynosi    więc energia pola magne

tycznego zawarta w rozpatrywanym obszarze elementarnym jest równa

iii^l

dW_m=\nH²2nlxdx=-. .x³d.x.    (6.59)

4n r%

finergię pola magnetycznego zawartą w przewodzie otrzymamy, całkując powyższe wymieni e w granicach od 0 do r₀, czyli

ro

(6.60)

IndukcyjnoŚć wewnętrzną L_w przewodu związaną z polem magnetycznym wewnątn przewodu oblicza się na podstawie wzoru (6,46):    ^

U²

Br.

(6.61)

Stwierdzamy, że indukcyjność wewnętrzna przewodu nie zależy od jego rozmiarów poprzecznych.