Image0087 BMP

a w granicy, gdy Az-*0, otrzymujemy

d//_ dV	(9.55)
przy uwzględnieniu, że Jy = yE>. Eliminując Ey z równań (9.54) i (9.55), znajdujemy dr^2	(9.56)
gdzie: k = yj)<i)fiy= ^1 (1+j), a	(9-57)
przy czym ux.	(9.58)
V oj/jy Rozwiązanie równania różniczkowego (9.56) przybiera postać Hy = Axt~^kz + A2s^kz, O^z^h,	(9.59)

gdzie: A_x, A₂ są stałymi całkowania.

W cełu ustalenia warunków brzegowych rozpatrzymy przewód n, licząc od dna żłobka. Dla krzywej zamkniętej, która częściowo przebiega w środowisku stalowym (krzywa C na rys. 9.7), a częściowo na dolnej powierzchni przewodu n, mamy na podstawie prawa przepływu

oH«|.-o+ jH-dl=(n-l)i,    (9.60)

c

bowiem wnętrze tej krzywej zamkniętej przenika n— 1 przewodów, z których każdy przewodzi prąd /. Przyjmując, że środowisko ferromagnetyczne jest nienasycone, można pominąć napięcie magnetyczne wzdłuż krzywej C, wobec czego natężenie pola magnetycznego w punktach dolnej powierzchni przewodu n jest równe

H,

o —

n -1

J.

a ~

(9.61)

W podobny sposób znajduje się natężenie pola magnetycznego w punktach górnej powierzchni rozpatrywanego przewodu, a mianowicie

|=-*=“    (9.62)

Wyrażenia (9.61) i (9.62) przedstawiają warunki brzegowe dla omawianego zagadnienia. Na podstawie ustalonych warunków brzegowych otrzymujemy równania

n — 1

A,+A_z = - I, a

/ł,e‘‘^fc + zł₃e^k" = -/,

a ~

Gęstość prądu obliczamy na podstawie zależności (9.55); mamy kJ nchfcz—(n —l)chfc(ft —z)

(9.64)

0

Llóre po rozwiązaniu dują

I <«— l)c^J

,U

¹ 2 a    sh kh

_1 n—(h — l)e~*^fl

² 2a    sh kh

Po podstawieniu tych stałych do wyrażenia (9.59), otrzymujemy

/ (n-l)shk(h-z) + nshkz

sh kh

(9.63)

sti kh

Jeżeli żłobek zawiera jeden przewód, to we wzorze (9.64) przyjmujemy « = 1. W przypadku, gdy żłobek zawiera dwa przewody, wówczas przyjmując n=2, a następnie «=1, otrzymujemy wzory dotyczące odpowiednio przewodu górnego i dolnego. Wykres modułu gęstości prądu dla obu tych przypadków przedstawia rys. 9.8. Stwierdzamy, że rozkład prądu w przewodzie charakteryzuje się dużą nierównomiemością.

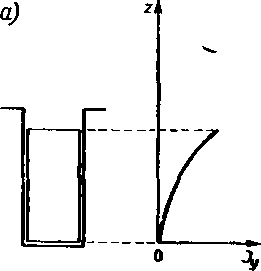
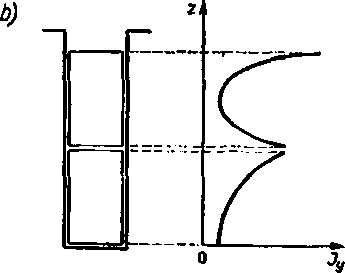
Rys. 9.8. Rozkład gęstości prądu w przewodach (a, b)

Na podstawie otrzymanych wyników można obliczyć moc czynną przekształcaną na ciepło w przewodzie, a następnie jego rezystancję przy prądzie sinusoidalnym.

Wektor Poyntinga w dow-otnym punkcie przewodu wyraża się wzorem

E x H* = Ej [i*\, x 1,=Ę, H*(-1.),

wobec czego przepływ mocy odbywa się w ujemnym kierunku osi Oz. W tych warunkach strumień mocy przepływa zarówno przez powierzchnię górną przewodu jak też i przez powierzchnię dolną, a moc zespolona związana z obszarem wewnętrznym przewodu n równa się różnicy strumieni mocy przez powierzchnię górną i dolną, czyli

(9.65)

S=al[E,Hj\^_h-E_yH*\_T-_₀-},

gdzie: / jest długością odcinka przewodu.