Nowe skanowanie 20080122080343 00000001C

W przypadku granicznym, gdy między cewkami nie ma sprzężenia, otrzymujemy znany wzór na impedancję dwu gałęzi równoległych

^ _ — 1—2_

Z1+Z2

Jeżeli obie cewki są połączone przeciwsobnie, tj. tak, że zaciski jednakoimienne cewek są połączone z różnymi węzłami (rys. 17.7), równania (17.13) i (17.14) przybierają następującą postać

U=Z₁I_l-Z_MI₂

U— ^ZmIi+ZzIz

skąd wyznaczamy prądy 7, i /₂

/i =

h =

Z₂ +Z\t

Z_lZ2-Zu

Zl + Z-M

z.Zz-zl

u

u

a następnie prąd wypadkowy J _ Zł + Z₂ + 2Z_M y

Z\Zz~Zm

Impedancja zastępcza układu równoległego

z = ZiZ2-Ź^    (17.17)

Z\ "+Zt2 “+ ZZm

Ten sam wynik można otrzymać podstawiając we wzorze (17.16) — Z_u zamiast Z_M.

Przykład 17.2. Dwie jednakowe cewki o rezystancjach Ry = Rz = 1 D, reaktancjach a>L y = = mL₂ — 10 £1 i 10M — 5 £1 połączono równolegle. Jaka jest impedancja zastępcza układu, w razie gdy:

a)    cewki są połączone zgodnie;

b)    cewki są połączone przeciwsobnie.

Rozwiązanie. Zy — Z% — 1+jlO; Z_M = j5

Impedancja zastępcza w przypadku zgodnego połączenia cewek:

7 = (1+jlO) (1+jlO)—(j5)² _ — 74+j20 ₌ (—74+j20) (2—jlO) ₌ . ₅ ,    -

1 +jl0 +1 + jl0—2-j5    2+jlO    104

Impedancja zastępcza w przypadku przeciwsobnego połączenia cewek

Z ₌ (1+jlO) (1+jlO)—(j5)^ł ₌ —74+j20 ₌ (-74+120) (2—j30) ₌ Q 5Mj2 5 l+jlO + l+jlO + 2-j5    2+j30    904    ’

Pytania

1.    Wyprowadzić wzory na impedancję zastępczą układu szeregowego dwóch cewek o parametrach Ri, Li i R₂, 1.2 o indukcyjności wzajemnej M przy połączeniu: a) zgodnym; b) przeciwsohnym.

2.    Jaka jest wartość zespolona impedancji sprzęgającej przy indukcyjności wzajemnej M i częstotliwości f?

3.    Kiedy w układzie szeregowym dwóch cewek prąd wyprzedza w fazie napięcie na jednej z cewek ?

4.    Wyprowadzić wzory na impedancję zastępczą dwóch gałęzi równoległych o impedancjach Zu Z2 i impedancji sprzęgającej Z_M przy połączeniu: a) zgodnym; b) przeciwsohnym.

5.    Kiedy w jednej z dwóch sprzężonych magnetycznie gałęzi nie płynie prąd (por. wyrażenia na lu Lz ^we wzorze \1.\5) ?

17.4. OBLICZANIE OBWODÓW ELEKTRYCZNYCH SPRZĘŻONYCH MAGNETYCZNIE

Przy obliczaniu obwodów elektrycznych posługujemy się prawami Kirchhoffa, bądź równaniami wyprowadzonymi z tych praw. W przypadku, gdy obwód elektryczny zawiera elementy sprzężone magnetycznie, należy w równaniach drugiego prawa Kirchhoffa    (E, U) = 0 uwzględniać wpływ sprzężeń magnetycznych na napięcia

występujące na danych elementach.

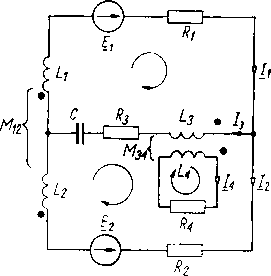
Rys. 17.8. Obwód elektryczny złożony, zawierający elementy sprzężone magnetycznie

Zastosowanie równań Kirchhoffa i równań Oczkowych do obwodów elektrycznych sprzężonych magnetycznie objaśnimy na konkretnym przykładzie (rys. 17.8).. Równania Kirchhoffa

h = h+ Iz

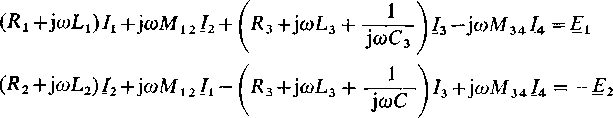
(■^4    JCłjA/34.^3 — 0

521