Str 097

Obliczymy elementy wzoru wyjściowego w funkcji h:

F = (3 + 2h)h,

_R = _F ₌ (3 + 2h)h °_z 3 + 2\[5h

Po zestawieniu obliczonych elementów otrzymamy bardzo złożone równanie z niewiadomą h. Najprościej można je rozwiązać, z pewnym przybliżeniem, następującą metodą: dla paru wartości h obliczymy wielkości F, O_z, R_h i iloczyny F.

h	F	O,	K	FRf
1	5	IM	0,67	3,82
2	14	11,94	1,17	15,54
1,5	9	9,70	0,93	8,56
1,4	8,1	9,25	0,875	7,40
1,45	8,55	9,47	0,90	7,96

W ten sposób określiliśmy głębokość wody w kanale z dostateczną dokładnością.

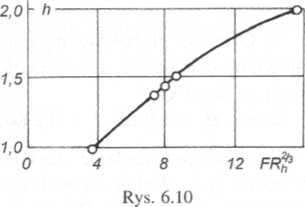
Rozwiązanie równania metodą kolejnych przybliżeń można przyspieszyć rnzez wykonanie (rys. 6.10) wykresu zależności FR%³ od h po obliczeniu już rzęch pierwszych punktów. Pozwala on na dość dokładne znalezienie wartości h odpowiadającej wartości FR_h =8.

Zadanie to można również rozwiązać korzystając z nomogramu (rys. 6.2).

Ponieważ znamy wartość modułu K =    = 8, więc dla tej wartości oraz

ii

b - 3m odczytujemy głębokość napełnienia h ~ 1,45.

4. Kanał ziemny ma mieć przekrój trapezowy o nachyleniu skarp 1 :3 : polu F = 20m³. Dobrać najkorzystniejszą hydraulicznie szerokość dna b :raz głębokość h (rys. 6.11).

Rozwiązanie:

F = (b + 3 h)h = 20,

Q_z = b + 2fi0h.

97