MATEMATYKA166

322 VI Ciągi i wręgi funkcyjni

I) f(\) xln() + x^J). m) f(x)=xln(.U2x), n) f(\) (x* l)ln(x 11).

322 VI Ciągi i wręgi funkcyjni

D r(x) = ln~5

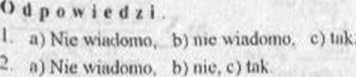
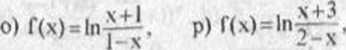
5 Tuk, nic wiadomo, nic wiadomo, nic; 2£r£4.

4. a) (-«,•**),    b) (-1/3.I/3),    c)(-<j,e),    d)(-4.4), c) (-^3c,l/3c),

l}{ *.-hx>),    g)(-4,4).    h)i ■ 1/c.l/c).    i) ( 4/3,4/3), j) f «o.-h»),

k) (-1/7.1/7),    1) <-!.!),    1) (-1/2,1/2),    m)(-c,c). n) (-3.3)

•V a) (-5.3), b)(-ac,+oc), c)(^:-Y4,-.Y4), d)(-oo,-Mo), e)(-c/3.c), 0(-/5,V5), K) (-=c.-c)u(c.+o&), h)( <*>,-1/e)u(l/c,+uc). i) (-<c,-2c/3)u(0.*x).

6.    a) (-oo,-h»). b) (-1/3,1/3). c)(~l,l), d) (-oo,+co), c) {OJ, 0 <-3/2,3/2),

g) < 1,1>> h)(-U>, i) <—1*1), j) (-U), k) (-cc.+oo), I) . I) (-1/4,1/4), m) <-1/2,1/2), n) <-l/2,l/2>, o) <-9.9), p)(-U), r) (-oo.+oc), s){0},

l) <-l/2,l/2>, u) (-2.2), V) (-1/2,1/2>. w) <-2,2>, z) (-1,1).

7.    a) (-1,0), b) (-2,2), c) (-2,0). d)< 3,0, c) (-oo,-f»). Q (-<*>,-«oT g) <-5/lX.-2/9>

h)    <-1,1/3). i) <-l/2,0), j) <-2.-l>, k) (-x,-2V<2.+-»), I) (-x,0>u<6,+ac), 1) (1/3.1), m) (-oo, l>u(l,+«). n) (5/3), o) ro/b dlu xeR, p) (-«,-!>ud/3.-f^), r) (-x,-3>^<3,4<»), s) <l/e,c). t) (0,c"V»(l. ■"»>., ' u) (-oo,-2>w<0.-wc),

v) (-<*>.+-»). w) {*/2+kx.k€C). z) <-*/4-fkJc.il/4-KkjeX keC.

8    l/()-fX') dla |\|<l; n) urctgx dlu |xfs 1, b) \urclgx dla Jx|i|. c) jc/4

9. l/(l-3x) dlu |x|< 1/3, a) 1/(1 3x)^:dla N)< 1/3. b) (6x-9x²)/(f-3x/dln |N,kl/3. c)2

10.

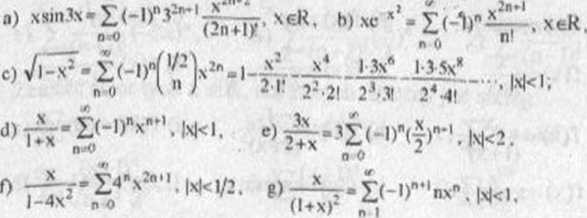
⁰⁾ '"T^T    • M*'.

n 0    n-0

p) bl|^=l..j. £    (i)*¹¹-<-})•• V^łl, x«-M>.

t» 0

2x-l

I 1

_v2n-2 n X

h) —-₂I< l)ⁿi<n-l)x.^{n :}. |.\J<1, i) xaretgx- EH/* ji^T ^|x,Sl’

(•■*■*)    ” n«2    n-V

j) xccw-4x.\02V (-I)¹*’¹. ■-- xrR,

fH ^(2n+2V

V)xarcsinx«x²+-J _x⁴+—n*-*-••. N<l,

1I2-3    2!2²-5    y 2^J-7

>•2

2n.l

l)    l*l-x²)»-££_, |x)<l, I) xln(lfx²). I(-l)^ft“Tr • W*l.

n ft ⁿ+^l    o o " '

m)    xln(3+2x)axln3lf £(-l)\ł)"^,|i£jl, _x€( 3/2.V2».

n 0

n)(x+l)ln(x+l)»*+ £(-1)" ■-

xⁿ**

(n+IXn+2)

, xe(-l.l>,

r)ln-*~U-ln3 T -l₇(2^n,1-(-i}^n>,)xⁿ-‘, xe< I/2.I/2).

"^X"‘    n=0ⁿ⁺    '

4. SZEREGI FOURIERA

SZEREGI TRYGONOMETRYCZNE Szeregiem trygonometrycznym nazywamy szereg postaci

(4 1)

^L(a_ncos^ + b

n 1

sin

gdzie t jest dowolnie ustaloną dodatnią liczbą rzeczywistą Wyrazy lego szeregu są Ainkcjami okresowymi o okresie 2t. Jeśli wice szereg len jest zbieżny na przedziale <-t,t >, lo jcsl on zbieżny na zbiorze R i suma tego szeregu jesl funkcją okresową o okresie 2t

TWIERDZENIE 4.1 Jeżeli szereg trygonometryczny (4 I) jcsl jednostajnie zbieżny na przedziale <-(,(> i jego suma jest równa f(x), to współczynniki a_n i b_n tego szeregu określone są tzw wzorami Eulera* Fouriera