32205 MATEMATYKA158

306 VI. Ciągi i szeregi funkcyjne

|q|<l o |—1<] <=> |xj<|x₀| o Hxol<x<|x₀|_t Xo

więc z nierówności (a) i kryterium porównawczego wynika, żc szereg Z|a_nxⁿ| jest zbieżny dla x e(-|x₀|,|x₀J).Oznacza lo, że szereg £a_nx" jest bezwzględnie zbieżny dla x e(-|x₀|,|x_o|).

D o w' ó d (2). Niech x e< -p_yp> i    Wówczas z nie

równości (a) wynika, żc

(b)    |a„x"|sM|f|"sM|-fr.

*0 ^X0

Szereg liczbowy |—f jest zbieżny jako geometryczny o ilorazie

^xo

q = |—1<1, więc szereg Ia_nxⁿ jest. zgodnie z kryterium Weierstrassa, ^xo

jednostajnie zbieżny na przedziale < -p,p>.

WNIOSEK 3.1. Jeżeli szereg potęgowy £a_nx^r jest rozbieżny w punkcie x, * 0, to jest rozbieżny dla x e(-x_ł-|x,|)u(|x,|,+QpV

Każdy szereg potęgowy Ia_nxⁿ jest zbieżny co najmniej dla x = 0. Jeśli ponadto jest zbieżny również w punkcie x₀ * 0, to jest zbieżny co najmniej na przedziale (-|x₀|,|x_ui)_ł symetrycznym względem x = 0. W celu znalezienia najdłuższego przedziału symetrycznego względem x = 0, wewnątrz którego szereg potęgowy jest zbieżny, wprowadzamy pojęcie promienia zbieżności

Promieniem zbieżności szeregu potęgowego Xa_nx" nazywamy:

1)    dodatnią liczbę r, tak dobraną, 2c dla |x|< r szereg ten jest zbieżny, a dla |x|> r szereg jest rozbieżny,

2)    liczbę r = 0. gdy szereg ten jest zbieżny jedynie dla x = 0,

3)    -4-00. gdy szereg ten jest zbieżny dla każdego x e (-x, +oc).

Jeżeli promień zbieżności szeregu potęgowego £a_nx" jest liczbą r > 0, to przedział (-r.r) nazy wamy przedziałem zbieżności tego szeregu. Jeżeli promień zbieżności jest równy +x. lo przedziałem zbieżności szeregu nazywamy przedział (-oo,+x)

METODY OBLICZANIA PROMIENIA ZBIEŻNOŚCI.

TWIERDZENIE 3.1 (Cauchy’ego) Jeżeli dla szeregu potęgowego £a_nx" istnieje skończona lub nieskończona granica

lim ^/iaj = g.

n-*»

to promień zbieżności tego szeregu jest równy

l/g, gdy 0<g<+*>,

(3.1)    r = < 0, gdy g = +»,

+QO, gdy g = 0

Dowód. Dla ustalonego x szereg la_nxⁿ jest szeregiem liczbowym. Zastosujmy kryterium Cauchy’cgo dla szeregów o wyrazach

dowolnych Obliczamy _

lim n/|a_#xⁿi=lim ^/|aj |x| = g |x|.

n~*x> *

Wiadomo, żc prawdziwe są implikacje: g|x| < 1 => Ia_nx" zbieżny oraz g|x| > 1 => Ia_nxⁿ rozbieżny.

1

1) Załóżmy, że g* 0. Wówczas dla tych x, dla których |x|< - szereg

O

Ia_nx^ft jest zbieżny, a dla tych x, dla których |x|> \ - szereg ten jest

D

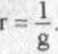
rozbieżny. Oznacza to, że promieniem zbieżności jest

2) Załóżmy, że g=0. Wówczas g|x|=0<l dla każdego x, zatem szereg Ia,x" jest zbieżny dla x €(-*>,+oo). Promień zbieżności tego szeregu jest więc równy +oo.

3) Załóżmy, żc g = +«. Wówczas g|x|=+oc dla każdego x *0, zatem szereg £a_nxⁿ jest rozbieżny dla każdego x*0, a zbieżny dla x=0. Oznacza to. że promień zbieżności tego szeregu jest równy r = 0.    P

TWIERDZENIE 3.2 (d Alembcrta). Jeżeli dla szeregu potęgowego Xa_Dxⁿ o współczynnikach a_n * 0 dla neN istnieje skończona lub nieskończona granica