MF dodatekA25

270 Podstawy matematyczne Aneks A

Przekształcając wzór A(6.1) i podstawiając y₀ dla wyznaczenia wartości przybliżonej x, otrzymujemy wzór

270 Podstawy matematyczne Aneks A

X=X|

+

yp-^f(^xi)

f(x₂)-f(xi)

(^x2-^xl)

A(6.4)

Podobnie jak poprzednio, w przypadku funkcji dwukrotnie różniczkowalnej w przedziale < Xi, x₂> błąd bezwzględny przybliżenia A(6.4) możemy oszacować na podstawie wzoru

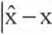
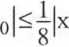
2

-x

3 M |f(^x2)-f(^xi)|

A(6.5)

A.7. Przybliżone metody rozwiązywania równań

W przypadku równań algebraicznych lub przestępnych niezmiernie rzadko udaje się znaleźć dokładną wartość ich pierwiastków. Stad metody przybliżonego rozwiązywania równań mają bardzo duże znaczenie w praktyce.

Niech dane będzie równanie

f(x) = 0 .    A(7.1)

Funkcja f(x) jest określona i ciągła w pewnym skończonym przedziale <a,b>.

Każdą wartość Xo, taką, że f(Xo)=0 nazywamy pierwiastkiem równania f(x)=0 lub miejscem zerowym funkcji f(x).

Obliczanie przybliżone pierwiastków równania A(7.1) dzielimy na dwa etapy:

1.    Lokalizacja pierwiastków - ustalenie możliwie małych przedziałów <a,b>, które zawierają dokładnie jeden pierwiastek,

2.    Uściślenie wartości pierwiastków przybliżonych - wyznaczenie tych pierwiastków z żądaną dokładnością.