skanuj0051 (55)

prostej sieciowej określonej przez parę węzłów odpowiada nieskończona liczba prostych równoległych przechodzących przez każdy węzeł, a każdej płaszczyźnie sieciowej odpowiada nieskończona liczba płaszczyzn o tej samej orientacji przechodzących przez każdy z tych węzłów. W takim przypadku mówi się o rodzinie płaszczyzn sieciowych (rys. 1.30). Pole płaskiej komórki sieciowej jest równe (rys. 1.31):

S = |axb| = absind

przy czym a i b oznaczają wektory, na których została zbudowana komórka. Pole prostej komórki płaskiej nie zależy od wyboru określających ją prostych. W istocie jest to powierzchnia przypisana każdemu z węzłów płaszczyzny.

Rys. 1.31. Powierzchnia komórki płaskiej = absind

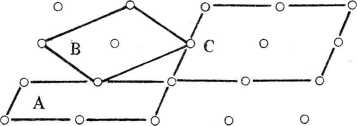
Rys. 1.32. Krotność komórek płaskich; A: n₁ — 0, n₂ = 2. komórka podwójna m = 2; B: n_x = 1, n₂ = 0, komórka podwójna m = 2; C: //, = 1, n₂ = 4, komórka poczwórna m — 4

Jeżeli komórka płaska wielokrotna zawiera n_x węzłów we wnętrzu i n₂ węzłów na bokach, a ponadto cztery węzły w wierzchołkach, to krotność komórki, tj. liczba zawartych w niej węzłów, jest równa (rys. 1.32):

m — 72₁ + 72₂/2 + 4/4

i jej powierzchnia jest m razy większa od powierzchni komórki prostej.

Objętość komórki trójwymiarowej jest określona przez mieszany iloczyn trzech wektorów, na których jest zbudowana komórka (rys. 1.33):

[abc] = a •( b x c) = 6-(cxa) = c • (a x b)

Objętość komórki prostej jest również niezmiennikiem; jest to oczywiście objętość przypisana każdemu węzłowi.

Objętość komórki wielokrotnej jest M razy większa od objętości komórki prostej, a M₉ krotność komórki, jest określona wyrażeniem

ⁿi + n₂/2+#3/4 + 8/8

55