Image36 (16)

159

Rozwiązania zadań ze zbioru "MENDLA

0,209

Q =-

Q = 5112

J m² mol • K

203000—

nr

8,3-7^—.

K ■ mol

J • J K • mol mol ■ K J

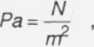
N-m = j

Q = 5,1 kJ

Odp.: Tlen pobrał 5,1 kJ ciepła.

Zadanie 665 str.132

Dane:    Szukane:

Ati = 25°C = AT 1 = 25 AC    .    ^^e = ?

—7 p = const. ^w

Qi = 500 J

At₂ = -75 °C = AT₂ = - 75 K

Q₂ = -1070 J    —^ V = const.

Z wyrażenia na ciepło molowe przy stałej objętości otrzymamy: Q

^Cv n • AT Q₂

^Cv " n • AT₂

Z wyrażenia na ciepło molowe przy stałym ciśnieniu mamy:

Q

^Cp n • AT Qi

^Cp “ n • ATi

Po podstawieniu otrzymamy:

Qi

c_p n • ATi ^{Cv _} Q2 n • aT₂

c_p Qi n • AT₂ c_v n • ATi Q₂ c^ _ Qi AT₂ c_v AT 1 Q₂ c^ _ Qi • AT₂ c_v Q₂ • AT₂

Rozwiązania zadań ze zbioru "MENDLA

160

Cp _ 500 J • ( - 75 K) Cv~ -1070 J ■ 25 K

Cr

Cv

1,4

Odp.: Stosunek ciepła molowego przy stałym ciśnieniu do ciepła molowego przy stałej objętości dla tlenku węgla wynosi 1,4.

Zadanie 666 str.132

Dane:

R = 8,31 ^ ^J . K ■ mol

n = 3 mole

AT = 80 K

k* 1,5

Szukane:

AU = ?

Zgodnie z I zasadą termodynamiki AU = Q + W

Zakładamy, że proces zachodzi w stałej objętości, więc praca W = 0, a ciepło molowe c_v możemy wyrazić wzorem:

Q    ,    . -r

Cv =-7^:    /• n • AT

n • AT

stąd Q = c_v • n • AT

Zmiana energii wewnętrznej przyjmie postać:

AU = c_v • n • AT

Nie znamy c_v, ale możemy je obliczyć z wykładnika adiabaty k.

Ponieważ k=^ /-c_v Cv

stąd k • c_v = c_p , ale c_p - c_v = R

więc c_p = R - Cv Po podstawieniu za c_p mamy:

K • Cv — R + Cy K • Cy ~ C_V = R

Cv • (K - 1) = R /: (K - 1)

stąd Cy = —^R „

K - 1

Po podstawieniu do wyrażenia na zmianę energii wewnętrznej będzie:

AU =

_R_ k- 1

8,31

n • AT J

AU =

K ■ mol

1,5-1

■ 3 mole ■ 80 K