Image41 (20)

169_Rozwiązania zadań ze zbioru "MENDLA"___

Objętość gazu zmieniła się proporcjonalnie do jego temperatury, więc gaz poddano przemianie izobarycznej p = const, a więc mamy zależność:

Vi_V2

Ti “T₂

Vi • T₂ = V₂ • Ti /: Ti

stąd V₂ =

V1 • T₂ Ti

Z wyrażenia na pracę gazu otrzymamy

W = — p • AV, gdzie AV = (V₂-Vi) skąd W = - po • (V₂ - V1)

...    Vi • T_{2 w}

W = - p₀ • (—--Vi)

_Vl.T₂-ViT_K

W = - Po •-^-)

i p = po

W = — po

Ti

Vi • (T₂-Ti)

P_a--tL

^Pa~n?

_______    ___(450 K- 300 K)

W = - 200000 Pa • 0,01 rrf •¹-²

N ■ m= J

W = - 1000 J = -1 kJ- minus oznacza, że pracę wykonał gaz (układ).

Odp.: Gaz wykonał pracę 1 kJ.

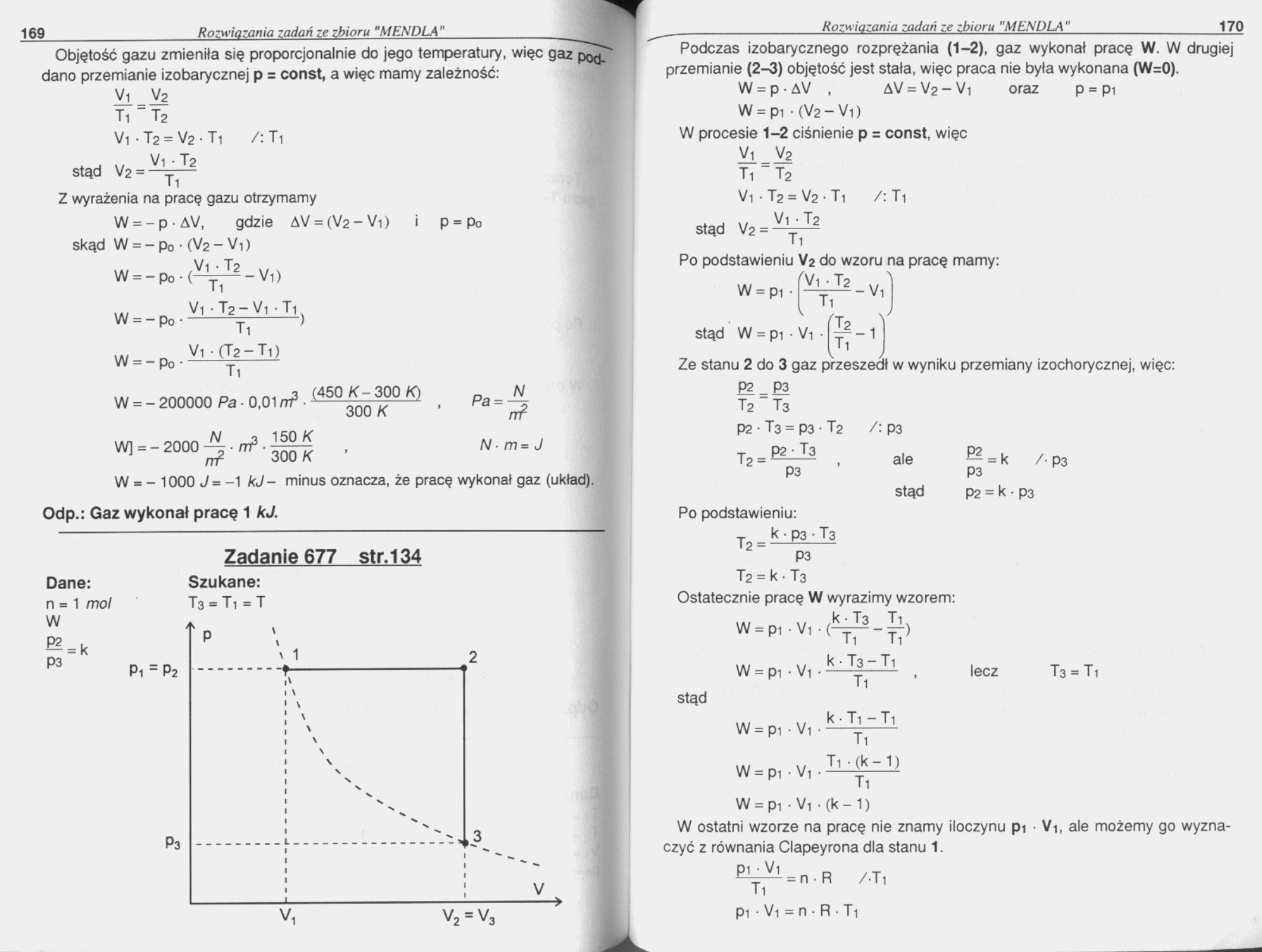
Zadanie 677 str.134

Dane:

n = 1 mol W

*-k

P3

Szukane:

T₃ = Ti = T

Pi ~ P2

P₃

P \	1	2
	P ^1\ \ \ \ \ \ \ \ \ V X V V	.3
		-----^ / / / / / < ' /

v₂ = v₃

V,

Podczas izobarycznego rozprężania (1-2), gaz wykonał pracę W. W drugiej przemianie (2-3) objętość jest stała, więc praca nie była wykonana (W=0).

W = p • AV ,    AV = V₂- Vi oraz p = pi

W = pi • (V₂-V1)

W procesie 1-2 ciśnienie p = const, więc Yi_V2 Ti ^_T₂

Vi • T₂ = V₂ • Ti /: Ti

stąd V₂-^

Ti

Po podstawieniu V₂ do wzoru na pracę mamy:

W = pi

Ti

^/V1*^T2V

stąd W = pi • Vi

Ze stanu 2 do 3 gaz przeszedł w wyniku przemiany izochorycznej, więc: P2 P3

T₂ Ta

P2 • T3 = p3 • T2	/: P3
	ale	e?=k
P3		P3
	stąd	P2 = k • p3

/• P3

Po podstawieniu:

T₂ =

k • P3 • Tą P3

T₂ = k • T₃

Ostatecznie pracę W wyrazimy wzorem:

...    .. k-T3 Ti

w = p,-v,.(—-^1

stąd

W = pi • Vi

W = pi • Vi W = pi • Vi

k • Tą - Ti Ti ”

k-Ti-Ti

Ti

Ti • (k - 1)

lecz

T₃ = Ti

W = pi • Vi • (k - 1)

= n • R /-Ti

W ostatni wzorze na pracę nie znamy iloczynu pi • Vi, ale możemy go wyznaczyć z równania Clapeyrona dla stanu 1. pi • Vi Ti

pi • Vi = n • R • Ti